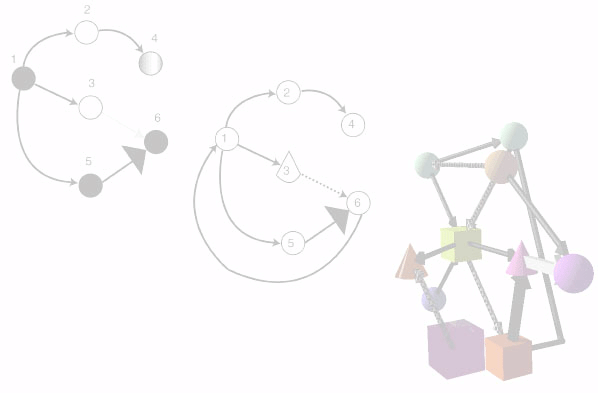The Lewis-McKinley Symbolic Language
A paper outlining the history and uses of systems created to symbolically convey information in concise forms, and which introduces a new method for doing so.
by
Clovice A. Lewis, Jr.
by
Clovice A. Lewis, Jr.
A picture is worth a thousand words... a story is worth a thousand pictures.
Click here for References and Links in this paper
Abstract
Human beings have engaged in the quest for meaning, and conveyance of meaning, for millennia. Systems of thought, language, imagery, and symbols have been created to assist us in communicating with one another. Much of what we refer to as language is so closely linked to the co-evolution of the human brain as to be virtually indistinguishable from how the mind actually works. Indeed, we are born already knowing about grammar and syntax before we learn our first word. As biological entities we respond to universal stimuli such as color, light, sound, texture, feeling, taste; and further up the chain of perception we experience memories and emotions. We communicate with each other in profoundly non-verbal means through the composition and performance of music, dance, and the visual arts. We are linked to the wisdom (and folly) of all people through the ages by the combined magic of writing and reading, with which we are able to vicariously occupy another's thoughts, control their emotions, or inflame their passions.
Whether explaining where and how far away from a cave our next potential meal is to a detailed explanation of the complex workings of an electronic circuit, we human beings have always relied on the method of telling stories as the best means of conveying information. In spite of many thousands of years of practice at it, transferring knowledge and information between us remains, in its essence, a time-consuming and laborious process for persons both sending and receiving. Yet systems for informing, training, and educating are burdened by ineffective paradigms of the past. This is largely because we rarely employ more than one method of communication at any one time, because we do not utilize the full spectrum of our senses when we do so, and because the time, energy, and cost to adequately prepare materials is asymmetrically high, especially when the information to be conveyed is subject to change.
The rapid pace of change has left many of us breathless. It is difficult to extract useful information from the ever-increasing onslaught of data. Systems of knowledge become more complicated, while our ability to understand those systems, the ways in which we communicate to each other about them, and the time we have to learn about them as opposed to their useful lives, shrink proportionally.
What is therefore needed is a method of conveying information that is universal, effective, powerful, allows for understanding on multiple levels, is cost-effective in its ability to provide an extremely high level and quality of documentation in a short period of time, and flexible enough to evolve with knowledge systems as they change. The method must allow people to understand complicated concepts by translating them into "stories" we can quickly assimilate.
This paper outlines the history of systems created to convey information in concise forms. It describes the use of symbology, logic, language, modeling, evolution, and systems theory as the basis for educational systems. This paper provides the theoretical framework for a proposed new method of presenting information called the Lewis-McKinley Symbolic Language (LMSL).
Human beings have engaged in the quest for meaning, and conveyance of meaning, for millennia. Systems of thought, language, imagery, and symbols have been created to assist us in communicating with one another. Much of what we refer to as language is so closely linked to the co-evolution of the human brain as to be virtually indistinguishable from how the mind actually works. Indeed, we are born already knowing about grammar and syntax before we learn our first word. As biological entities we respond to universal stimuli such as color, light, sound, texture, feeling, taste; and further up the chain of perception we experience memories and emotions. We communicate with each other in profoundly non-verbal means through the composition and performance of music, dance, and the visual arts. We are linked to the wisdom (and folly) of all people through the ages by the combined magic of writing and reading, with which we are able to vicariously occupy another's thoughts, control their emotions, or inflame their passions.
Whether explaining where and how far away from a cave our next potential meal is to a detailed explanation of the complex workings of an electronic circuit, we human beings have always relied on the method of telling stories as the best means of conveying information. In spite of many thousands of years of practice at it, transferring knowledge and information between us remains, in its essence, a time-consuming and laborious process for persons both sending and receiving. Yet systems for informing, training, and educating are burdened by ineffective paradigms of the past. This is largely because we rarely employ more than one method of communication at any one time, because we do not utilize the full spectrum of our senses when we do so, and because the time, energy, and cost to adequately prepare materials is asymmetrically high, especially when the information to be conveyed is subject to change.
The rapid pace of change has left many of us breathless. It is difficult to extract useful information from the ever-increasing onslaught of data. Systems of knowledge become more complicated, while our ability to understand those systems, the ways in which we communicate to each other about them, and the time we have to learn about them as opposed to their useful lives, shrink proportionally.
What is therefore needed is a method of conveying information that is universal, effective, powerful, allows for understanding on multiple levels, is cost-effective in its ability to provide an extremely high level and quality of documentation in a short period of time, and flexible enough to evolve with knowledge systems as they change. The method must allow people to understand complicated concepts by translating them into "stories" we can quickly assimilate.
This paper outlines the history of systems created to convey information in concise forms. It describes the use of symbology, logic, language, modeling, evolution, and systems theory as the basis for educational systems. This paper provides the theoretical framework for a proposed new method of presenting information called the Lewis-McKinley Symbolic Language (LMSL).
Knowledge Systems...The Foundation of Learning
A knowledge system is typically defined as a computer system programmed to imitate the problem-solving procedures of humans in a particular field of expertise. The success of a knowledge system depends on the quality of the data provided to the computer, and the rules programmed into the computer for making deductions from that data.
Knowledge systems, are based on two fundamental operations:
New incoming pieces of information must be assimilated into the knowledge base by means of an appropriate update operation. This includes simple insertion of new information and deletion of old information. The update operation should satisfy some principle of minimal change or minimal mutilation.
Questions posed to the knowledge base must be answered by means of an inference operation. The inference operation should be complete with respect to some well-understood logic, and sound with respect to a preferential entailment relation in that logic[1].
The term "Knowledge System" is increasingly being used to apply in non-computer domains, such as social, economic[2], and governmental systems. In a Ph.D. dissertation entitled "Information Sources of Agricultural Extension Specialists in Indonesia", Paul Mundy elucidates four reasons why the exchange of information in an agricultural knowledge system is lacking[3]. His analysis sites arithmetic, distance, translation, and adaptation... certainly non-standard terms used to describe a particular problem with the "exchange of information vital to the smooth functioning of such systems." His work is cited here to illustrate how terminology usually found in computer, cybernetics, system theory, and logic fields are used to describe complex human concepts.
Essential to knowledge systems is the quality of information conveyed to the entity (person or computer) that must use it, how the entity acts on the information, and how the entity learns from the information in making self-sufficient decisions and/or acting autonomously in a given environment. Herein lies the building blocks of learning. Knowledge must be acquired, it must be stored, it must be shared, and it must be used. Strategies for analyzing and applying knowledge systems are represented by the fields of ontology, Artificial Intelligence, and cybernetics.
Ontology
The word "ontology" has a long history in philosophy, in which it refers to the subject of existence. It is sometimes confused with epistemology, which is about knowledge and knowing.
The term ontology is commonly used to mean a specification of a conceptualization in the context of knowledge sharing. Used thus, an ontology is a description of the concepts and relationships that can exist for an agent or a community of agents. An ontology can be viewed as a set of concept definitions. Put simply, it is a specification of a conceptualization.
Software engineers have been designing ontologies for the purpose of enabling knowledge sharing and reuse of information. In this context, an ontology is a specification used for making ontological commitments. For pragmatic reasons, they choose to write an ontology as a set of definitions of formal vocabulary. Although it is not the only way to specify a conceptualization, it has desirable properties for knowledge sharing among developers of Artificial Intelligence software. For software designers, an ontological commitment is an agreement to use a vocabulary (i.e., ask questions and make assertions) in a way that is consistent (but not complete) with respect to the theory specified by an ontology. Software engineers build agents that commit to ontologies. They design ontologies so they can share knowledge with and among these agents.[4]
Ontology is currently employed in the engineering realms of Artificial Intelligence, intelligent enterprises, and database systems. In all cases, the ability to provide a common basis for understanding key terms and concepts is necessary to ensure consistent information.[5] A group of scholars and research scientists operating at the LADSEB-CNR, University of Padova, Italy describes itself as a group which "performs basic and applied research on the ontological foundations of knowledge engineering and conceptual modeling, exploring the role of ontology in knowledge representation, database design, information retrieval, natural-language processing, multi-agent systems, software engineering, and information systems in general. The group is characterized by a strong interdisciplinary approach that combines Computer Science, Philosophy, and Linguistics, and relies on Logic as a unifying paradigm."[6]
Artificial Intelligence
Artificial Intelligence (AI) is the ability of an artificial mechanism to exhibit intelligent processes. These processes include learning, reasoning, and self-correction. AI has shown great promise in the area of knowledge-based expert programs, which, although powerful when utilized within a specific domain, are at present incapable of adaptable, or truly intelligent, reasoning.
The British computer scientist Alan Turing, an early scientist in the field, stated that a computer would earn the title as an intelligent machine when and if it could deceive a human into believing that it was human. He wrote a paper in 1950 describing what is now known as the "Turing Test". Turing's paper describing the test has been used in countless journals and papers relating to machine intelligence. The 1987 edition of the Oxford Companion to the Mind describes the Turing test as "the best test we have for confirming the presence of intelligence in a machine."[7]
A knowledge system is typically defined as a computer system programmed to imitate the problem-solving procedures of humans in a particular field of expertise. The success of a knowledge system depends on the quality of the data provided to the computer, and the rules programmed into the computer for making deductions from that data.
Knowledge systems, are based on two fundamental operations:
New incoming pieces of information must be assimilated into the knowledge base by means of an appropriate update operation. This includes simple insertion of new information and deletion of old information. The update operation should satisfy some principle of minimal change or minimal mutilation.
Questions posed to the knowledge base must be answered by means of an inference operation. The inference operation should be complete with respect to some well-understood logic, and sound with respect to a preferential entailment relation in that logic[1].
The term "Knowledge System" is increasingly being used to apply in non-computer domains, such as social, economic[2], and governmental systems. In a Ph.D. dissertation entitled "Information Sources of Agricultural Extension Specialists in Indonesia", Paul Mundy elucidates four reasons why the exchange of information in an agricultural knowledge system is lacking[3]. His analysis sites arithmetic, distance, translation, and adaptation... certainly non-standard terms used to describe a particular problem with the "exchange of information vital to the smooth functioning of such systems." His work is cited here to illustrate how terminology usually found in computer, cybernetics, system theory, and logic fields are used to describe complex human concepts.
Essential to knowledge systems is the quality of information conveyed to the entity (person or computer) that must use it, how the entity acts on the information, and how the entity learns from the information in making self-sufficient decisions and/or acting autonomously in a given environment. Herein lies the building blocks of learning. Knowledge must be acquired, it must be stored, it must be shared, and it must be used. Strategies for analyzing and applying knowledge systems are represented by the fields of ontology, Artificial Intelligence, and cybernetics.
Ontology
The word "ontology" has a long history in philosophy, in which it refers to the subject of existence. It is sometimes confused with epistemology, which is about knowledge and knowing.
The term ontology is commonly used to mean a specification of a conceptualization in the context of knowledge sharing. Used thus, an ontology is a description of the concepts and relationships that can exist for an agent or a community of agents. An ontology can be viewed as a set of concept definitions. Put simply, it is a specification of a conceptualization.
Software engineers have been designing ontologies for the purpose of enabling knowledge sharing and reuse of information. In this context, an ontology is a specification used for making ontological commitments. For pragmatic reasons, they choose to write an ontology as a set of definitions of formal vocabulary. Although it is not the only way to specify a conceptualization, it has desirable properties for knowledge sharing among developers of Artificial Intelligence software. For software designers, an ontological commitment is an agreement to use a vocabulary (i.e., ask questions and make assertions) in a way that is consistent (but not complete) with respect to the theory specified by an ontology. Software engineers build agents that commit to ontologies. They design ontologies so they can share knowledge with and among these agents.[4]
Ontology is currently employed in the engineering realms of Artificial Intelligence, intelligent enterprises, and database systems. In all cases, the ability to provide a common basis for understanding key terms and concepts is necessary to ensure consistent information.[5] A group of scholars and research scientists operating at the LADSEB-CNR, University of Padova, Italy describes itself as a group which "performs basic and applied research on the ontological foundations of knowledge engineering and conceptual modeling, exploring the role of ontology in knowledge representation, database design, information retrieval, natural-language processing, multi-agent systems, software engineering, and information systems in general. The group is characterized by a strong interdisciplinary approach that combines Computer Science, Philosophy, and Linguistics, and relies on Logic as a unifying paradigm."[6]
Artificial Intelligence
Artificial Intelligence (AI) is the ability of an artificial mechanism to exhibit intelligent processes. These processes include learning, reasoning, and self-correction. AI has shown great promise in the area of knowledge-based expert programs, which, although powerful when utilized within a specific domain, are at present incapable of adaptable, or truly intelligent, reasoning.
The British computer scientist Alan Turing, an early scientist in the field, stated that a computer would earn the title as an intelligent machine when and if it could deceive a human into believing that it was human. He wrote a paper in 1950 describing what is now known as the "Turing Test". Turing's paper describing the test has been used in countless journals and papers relating to machine intelligence. The 1987 edition of the Oxford Companion to the Mind describes the Turing test as "the best test we have for confirming the presence of intelligence in a machine."[7]
Alan Turing
The term Artificial Intelligence was coined in 1956, when a group of scientists met for a summer workshop. Attending was Allen Newell, Herbert Simon, Marvin Minsky, Oliver Selfridge, and John McCarthy, among others. Their early work in AI consisted of attempts to simulate the neural networks of the brain with numerically modeled nerve cells called perceptrons. During the early 1960s, Newell, Simon, and J. C. Shaw developed the "logical theorist" computer program, which introduced symbolic processing. Instead of constructing systems based on numbers, they built systems that manipulated symbols. This powerful approach forms the basis of most work in AI to the present. Symbol manipulation is expressed as rules, for example, "If y is a airplane, then y can fly." If such an AI system determines or is told that a Boeing 747 is an airplane, then it can infer that the Boeing 747 can fly.
The field of AI was born when the concept of universal computation [Turing 1936], the cultural view of the brain as a computer, and the widespread availability of digital computing machines were combined.
Marvin Minsky addressed one of the philosophical speculations about what constitutes the mind or intelligence generated by the field of AI:
"When intelligent machines are constructed, we should not be surprised to find them as confused and as stubborn as are men in their convictions about mind-matter, consciousness, free will, and the like. For all such questions are pointed at explaining the complicated interactions between parts of the self-model. A man's or a machine's strength of conviction about such things tells us nothing about the man or about the machine except what it tells us about his model of himself." [8]
The term Artificial Intelligence was coined in 1956, when a group of scientists met for a summer workshop. Attending was Allen Newell, Herbert Simon, Marvin Minsky, Oliver Selfridge, and John McCarthy, among others. Their early work in AI consisted of attempts to simulate the neural networks of the brain with numerically modeled nerve cells called perceptrons. During the early 1960s, Newell, Simon, and J. C. Shaw developed the "logical theorist" computer program, which introduced symbolic processing. Instead of constructing systems based on numbers, they built systems that manipulated symbols. This powerful approach forms the basis of most work in AI to the present. Symbol manipulation is expressed as rules, for example, "If y is a airplane, then y can fly." If such an AI system determines or is told that a Boeing 747 is an airplane, then it can infer that the Boeing 747 can fly.
The field of AI was born when the concept of universal computation [Turing 1936], the cultural view of the brain as a computer, and the widespread availability of digital computing machines were combined.
Marvin Minsky addressed one of the philosophical speculations about what constitutes the mind or intelligence generated by the field of AI:
"When intelligent machines are constructed, we should not be surprised to find them as confused and as stubborn as are men in their convictions about mind-matter, consciousness, free will, and the like. For all such questions are pointed at explaining the complicated interactions between parts of the self-model. A man's or a machine's strength of conviction about such things tells us nothing about the man or about the machine except what it tells us about his model of himself." [8]
Marvin Minsky
Cybernetics
Cybernetics is a term used to describe the science of control and communication in animals, humans, machines, and organizations. Coined by mathematician Norbert Wiener in 1946, the word cybernetics is derived from the Greek kybernetes, which means "steersman." The original concept grew out of Wiener's and his colleague Julian Bigelow's work on antiaircraft guns during World War II, making use of the concept of feedback -- the feeding back of operating data into a system from the interactions of the system with the environment.
Early work in cybernetics focused on the use of feedback by servomechanisms and other forms of automation. Later, in collaboration with physiologist Arturo Rosenblueth, Wiener showed that cybernetics could also be used to analyze the human nervous system. Cybernetics thus eventually attracted the interest of psychologists and psychiatrists. Another major factor in the development of the field came from computer science, where computers could model the nervous system, as well as being used as a tool for developing and studying models of other complex systems (Artificial Intelligence).
Four basic principles are central to cybernetics theories: variety, circularity, process and observation. Variety is fundamental to its information, communication and control theories and emphasizes multiplicity, choices, and intelligence rather than force and singular necessity. Circularity occurs in its earliest theories of circular causation or feedback. Most all cybernetic theories involve process and change, from its notion of information, as the difference between two states of uncertainty, to theories of adaptation, evolution and growth processes. A special feature of cybernetics is that it explains such processes in terms of the organization of the system in terms of feedback loops used for regulation and a system's effort to maintain an equilibrium or to reach a goal. Observation, including decision making is the process underlying cybernetic theories of information processing and computing.[9]
Cybernetics
Cybernetics is a term used to describe the science of control and communication in animals, humans, machines, and organizations. Coined by mathematician Norbert Wiener in 1946, the word cybernetics is derived from the Greek kybernetes, which means "steersman." The original concept grew out of Wiener's and his colleague Julian Bigelow's work on antiaircraft guns during World War II, making use of the concept of feedback -- the feeding back of operating data into a system from the interactions of the system with the environment.
Early work in cybernetics focused on the use of feedback by servomechanisms and other forms of automation. Later, in collaboration with physiologist Arturo Rosenblueth, Wiener showed that cybernetics could also be used to analyze the human nervous system. Cybernetics thus eventually attracted the interest of psychologists and psychiatrists. Another major factor in the development of the field came from computer science, where computers could model the nervous system, as well as being used as a tool for developing and studying models of other complex systems (Artificial Intelligence).
Four basic principles are central to cybernetics theories: variety, circularity, process and observation. Variety is fundamental to its information, communication and control theories and emphasizes multiplicity, choices, and intelligence rather than force and singular necessity. Circularity occurs in its earliest theories of circular causation or feedback. Most all cybernetic theories involve process and change, from its notion of information, as the difference between two states of uncertainty, to theories of adaptation, evolution and growth processes. A special feature of cybernetics is that it explains such processes in terms of the organization of the system in terms of feedback loops used for regulation and a system's effort to maintain an equilibrium or to reach a goal. Observation, including decision making is the process underlying cybernetic theories of information processing and computing.[9]
Symbolic Modeling
"Man lives in a world of ideas. Any phenomenon is so complex that he cannot possibly grasp the whole of it. He abstracts certain characteristics of a given phenomenon as an idea, then represents that idea as a symbol, be it a word or a mathematical sign. Human reaction is almost entirely to symbols, and only negligibly to phenomenon. As a matter of fact," he continued, removing the cigarette holder from his mouth and settling into his subject, "it can be demonstrated that the human mind can only think in terms of symbols." - Robert Heinlein, "Blowups Happen", 1939
Symbolic Modeling systems are high-level computer languages (such as LISP, and PROLOG) that are useful in applications requiring knowledge processing, such as expert systems and Artificial Intelligence. They are called symbolic languages because they use symbols (actually words) to represent concepts. Computer-based symbolic modeling systems manipulate these symbols (called atoms) in ways that resemble logical reasoning or inference.
In engineering and science, models are descriptive (of the entities of a system, their attributes and their relationships), and models are predictive (of the values of dependent system attributes following change in independent attribute values). Symbolic (Non-numeric) models are now used to formalize, describe, and analyze complex processes, devices and systems. AI techniques now allow development of non-numeric ("symbolic") tools to analyze systems qualitatively. Thus, symbolic modeling allows development of principled models of qualitative engineering processes, such as estimation, planning, and design.
The spill-over of techniques and methods of Symbolic Modeling (as with Cybernetics and AI) to other disciplines has increased tremendously in recent years. Examples of the use of modeling techniques are briefly noted in the following paragraphs.
Political Systems
A method of computational politics called Polimetrics was advanced by Alker (1975), to illustrate formal modeling techniques for political science. Alker stated (1975: 147),
"... polimetrics is the application of mathematical forms and statistical techniques [or procedures] to [the qualitative labeling and quantitative metricizing of possibly observable] political phenomena, the scientific testing of political theories, and the solution of present and future political problems."
Although this definition leans toward quantitative methods based on behaviorally observable data, it is sufficient to cover symbolic modeling techniques. Not surprisingly, Alker includes within polimetrics other computation-related methods such as game theory and cognitive models based on "conceptual dependency".
A concise definition of Polimetrics is offered by John C. Mallery: "...computational politics refers to the technique and practice of formulating, implementing, interpreting, and evaluating computational models of political phenomena."[10]
Psychology
The field of psychology has embraced Symbolic Modeling techniques. Joseph O'Connor and John Seymour define modeling as "The process of discerning the sequence of ideas and behavior that enable someone to accomplish a task."[11] Robert Dilts offers another definition, "The process of observing and mapping the successful behaviors of other people."[12] Put very simply, Symbolic Modeling in psychological terms, is a process that happens over time, it involves the observation of someone who is achieving something, and involves the creation of a model of what they are doing. The term NLP (Neuro-Linguistic Programming) is used to describe the modeling process.
Linguistic metaphors are traditionally used in NLP, and are explained by Connor and Seymour as:
"Indirect communication by a story or figure of speech implying a comparison. It covers similes, parables and allegories."[13]
The influence of cybernetic systems, computational theories, symbolic mapping, and the like are easily seen in an explanation of symbolic representation of information encoded in human visual, auditory, and kinesthetic biology in the following quote from Robert Dilts:
"It is also important to recognize that, in addition to being able to input, process, and output information, all representational systems have the capability to represent information in at least two ways: literally and figuratively. That is, each of our sensory systems can form maps that have either a direct correspondence or a more metaphorical correspondence to the phenomenon we are representing. For example, we can visualize the white cells of our bodies as we have seen them under the microscope, or as looking like octopi or 'Pac-Man' video game characters. Similarly, we can speak of our brains literally as 'a network of neurons,' or figuratively as being 'like a computer.' Likewise, we can experience a particular emotional symptom as a particular set of kinesthetic body sensations or as a 'knot' in the stomach."[14]
The Limits of Logic
"When we think, we let symbols operate on other symbols in certain, set fashions - rules of logic, or rules of mathematics. If the symbols have been abstracted so that they are structurally similar to the phenomena they stand for, and if the symbol operations are similar in structure and order to the operations of the phenomena in the real world, we think sanely. If our logic-mathematics, or our word-symbols, have been poorly chosen, we think not sanely." - Robert Heinlein, "Blowups Happen", 1939
This paper is primarily concerned with techniques (most especially visual techniques) employed to convey logic; arguably the life blood of digital electronics and present-day computers. Logic is the systematic study of reasoning that provides standards by which valid reasoning can be recognized. It clarifies the reasoning process and provides a means for analyzing the consistency of basic concepts. Mathematical logic achieves precision, clarity, and manipulability through the use of artificial languages, symbol systems deliberately constructed for use in logic. Sentence-like structures of such a system may represent sentences of natural languages like English, directly representing logical words such as "no" or "all", and suppressing structures considered irrelevant.[15]
An early pioneer of symbolic logic, and an inventor of symbology for conveying logic, was Thomas Harriot (1560-1621), an English mathematician and astronomer. His mathematical work included the introduction of simplified notation for algebra and research on the theory of equations. In a time when many of his contemporaries were being hanged for heretical notions, Harriot somehow managed to avoid this fate, while actively promoting such philosophies as Hermetic Kabbalism[16] (many scientist/alchemists of that time were Kabbalists). During this time great controversies raged about the role of the divine (specifically Jesus) in any system of abstraction. Under the auspices of Walter Raleigh, Harriot actually led an expedition to North America in 1584. His charter was to search for New World wisdom to revolutionize thought.[17] The result of his stay with a tribe of Native Americans was proof of the existence of a Kabbalah, or a system of logical abstraction, without a divinity (specifically Jesus). The notion of a religious-free system of abstraction and logic is, in this day, a non-issue. Such was not the case when Harriot was skirting the fires of a occult-unfriendly English courts.
The German philosopher and mathematician Gottfried Wilhelm von Leibniz (1716-1846) anticipated the development of symbolic logic and, independently of Isaac Newton, invented the calculus with a superior notation, including the symbols for integration and differentiation. It is interesting to note that he expounded a theory of substance based on "monads", which he explained as metaphysical and animistically endowed points of force and perception. Each monad was internally determined by its definition. Monads could not interact, but, due to a "preestablished harmony," the action in one monad coincided with that in another. Leibniz believed that the truths about monads could be discovered by rational analysis.
"Man lives in a world of ideas. Any phenomenon is so complex that he cannot possibly grasp the whole of it. He abstracts certain characteristics of a given phenomenon as an idea, then represents that idea as a symbol, be it a word or a mathematical sign. Human reaction is almost entirely to symbols, and only negligibly to phenomenon. As a matter of fact," he continued, removing the cigarette holder from his mouth and settling into his subject, "it can be demonstrated that the human mind can only think in terms of symbols." - Robert Heinlein, "Blowups Happen", 1939
Symbolic Modeling systems are high-level computer languages (such as LISP, and PROLOG) that are useful in applications requiring knowledge processing, such as expert systems and Artificial Intelligence. They are called symbolic languages because they use symbols (actually words) to represent concepts. Computer-based symbolic modeling systems manipulate these symbols (called atoms) in ways that resemble logical reasoning or inference.
In engineering and science, models are descriptive (of the entities of a system, their attributes and their relationships), and models are predictive (of the values of dependent system attributes following change in independent attribute values). Symbolic (Non-numeric) models are now used to formalize, describe, and analyze complex processes, devices and systems. AI techniques now allow development of non-numeric ("symbolic") tools to analyze systems qualitatively. Thus, symbolic modeling allows development of principled models of qualitative engineering processes, such as estimation, planning, and design.
The spill-over of techniques and methods of Symbolic Modeling (as with Cybernetics and AI) to other disciplines has increased tremendously in recent years. Examples of the use of modeling techniques are briefly noted in the following paragraphs.
Political Systems
A method of computational politics called Polimetrics was advanced by Alker (1975), to illustrate formal modeling techniques for political science. Alker stated (1975: 147),
"... polimetrics is the application of mathematical forms and statistical techniques [or procedures] to [the qualitative labeling and quantitative metricizing of possibly observable] political phenomena, the scientific testing of political theories, and the solution of present and future political problems."
Although this definition leans toward quantitative methods based on behaviorally observable data, it is sufficient to cover symbolic modeling techniques. Not surprisingly, Alker includes within polimetrics other computation-related methods such as game theory and cognitive models based on "conceptual dependency".
A concise definition of Polimetrics is offered by John C. Mallery: "...computational politics refers to the technique and practice of formulating, implementing, interpreting, and evaluating computational models of political phenomena."[10]
Psychology
The field of psychology has embraced Symbolic Modeling techniques. Joseph O'Connor and John Seymour define modeling as "The process of discerning the sequence of ideas and behavior that enable someone to accomplish a task."[11] Robert Dilts offers another definition, "The process of observing and mapping the successful behaviors of other people."[12] Put very simply, Symbolic Modeling in psychological terms, is a process that happens over time, it involves the observation of someone who is achieving something, and involves the creation of a model of what they are doing. The term NLP (Neuro-Linguistic Programming) is used to describe the modeling process.
Linguistic metaphors are traditionally used in NLP, and are explained by Connor and Seymour as:
"Indirect communication by a story or figure of speech implying a comparison. It covers similes, parables and allegories."[13]
The influence of cybernetic systems, computational theories, symbolic mapping, and the like are easily seen in an explanation of symbolic representation of information encoded in human visual, auditory, and kinesthetic biology in the following quote from Robert Dilts:
"It is also important to recognize that, in addition to being able to input, process, and output information, all representational systems have the capability to represent information in at least two ways: literally and figuratively. That is, each of our sensory systems can form maps that have either a direct correspondence or a more metaphorical correspondence to the phenomenon we are representing. For example, we can visualize the white cells of our bodies as we have seen them under the microscope, or as looking like octopi or 'Pac-Man' video game characters. Similarly, we can speak of our brains literally as 'a network of neurons,' or figuratively as being 'like a computer.' Likewise, we can experience a particular emotional symptom as a particular set of kinesthetic body sensations or as a 'knot' in the stomach."[14]
The Limits of Logic
"When we think, we let symbols operate on other symbols in certain, set fashions - rules of logic, or rules of mathematics. If the symbols have been abstracted so that they are structurally similar to the phenomena they stand for, and if the symbol operations are similar in structure and order to the operations of the phenomena in the real world, we think sanely. If our logic-mathematics, or our word-symbols, have been poorly chosen, we think not sanely." - Robert Heinlein, "Blowups Happen", 1939
This paper is primarily concerned with techniques (most especially visual techniques) employed to convey logic; arguably the life blood of digital electronics and present-day computers. Logic is the systematic study of reasoning that provides standards by which valid reasoning can be recognized. It clarifies the reasoning process and provides a means for analyzing the consistency of basic concepts. Mathematical logic achieves precision, clarity, and manipulability through the use of artificial languages, symbol systems deliberately constructed for use in logic. Sentence-like structures of such a system may represent sentences of natural languages like English, directly representing logical words such as "no" or "all", and suppressing structures considered irrelevant.[15]
An early pioneer of symbolic logic, and an inventor of symbology for conveying logic, was Thomas Harriot (1560-1621), an English mathematician and astronomer. His mathematical work included the introduction of simplified notation for algebra and research on the theory of equations. In a time when many of his contemporaries were being hanged for heretical notions, Harriot somehow managed to avoid this fate, while actively promoting such philosophies as Hermetic Kabbalism[16] (many scientist/alchemists of that time were Kabbalists). During this time great controversies raged about the role of the divine (specifically Jesus) in any system of abstraction. Under the auspices of Walter Raleigh, Harriot actually led an expedition to North America in 1584. His charter was to search for New World wisdom to revolutionize thought.[17] The result of his stay with a tribe of Native Americans was proof of the existence of a Kabbalah, or a system of logical abstraction, without a divinity (specifically Jesus). The notion of a religious-free system of abstraction and logic is, in this day, a non-issue. Such was not the case when Harriot was skirting the fires of a occult-unfriendly English courts.
The German philosopher and mathematician Gottfried Wilhelm von Leibniz (1716-1846) anticipated the development of symbolic logic and, independently of Isaac Newton, invented the calculus with a superior notation, including the symbols for integration and differentiation. It is interesting to note that he expounded a theory of substance based on "monads", which he explained as metaphysical and animistically endowed points of force and perception. Each monad was internally determined by its definition. Monads could not interact, but, due to a "preestablished harmony," the action in one monad coincided with that in another. Leibniz believed that the truths about monads could be discovered by rational analysis.
Gottfried Wilhelm von Leibniz Calculating machine invented by Leibniz (could divide and multiply)
Schemes for conveying logic ultimately (and very quickly) become enmeshed in complexity. Mathematicians, philosophers, scientists, and everyday folk need to, not only explain phenomenon, but possess models with which to pierce the veil of reality and even glimpse the future. It is no accident that thinkers such as Harriot, Leibniz, Einstein, and others find themselves creating systems that help humanity think more clearly, then become entangled in issues dealing with thought, symbols, and reality.
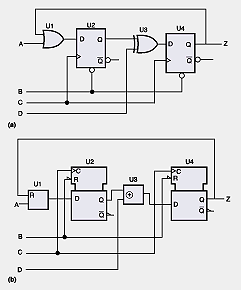
There are limits to logic, specifically First Order Logic (FOL), of the type that is used in many of the "hard sciences", where causal behavior can be reduced to fundamental well-founded primitives. Examples of symbology used to express FOL are the truth tables and logic gate representations in electronics. Symbols used in these schematics provide clear documentation of, not only the constituents of a circuit, but a picture of the operation of that circuit. A difficulty called the "completeness" problem exerts itself: to perform system-level analyses, one must model some critical mass of the system being studied. Electronic engineers constantly grapple with this problem because the symbology used to describe complex digital circuits cannot provide an adequate picture of their operation – the story of their miniature worlds are difficult to tell. Engineers are now being asked to develop hardware in a manner that is similar to high-level languages used to develop software. An article featured in EDD August 4, 1994 states the problem rather surprisingly:
"Unfortunately, a textual source listing of HDL (hardware description language) code doesn't provide all the information contained in a schematic's graphics. Although some of the graphical information is available--you have to provide names of interface signals and the directions of signal flows when you define VHDL (very-high-speed integrated circuits) components--other information doesn't easily fit into the HDL process. Signal feedback, locality, and sequenced vs parallel operation, for example, have no explicit graphical representation in HDL code. The HDL-development process must recognize these deficiencies and provide a means of compensation. When experienced circuit designers are just becoming familiar with HDL-based design, they often express a feeling of discomfort with the process. However, after being shown methods that compensate for information loss, they realize that information loss was the source of their discomfort." [18]
There are limits to logic, specifically First Order Logic (FOL), of the type that is used in many of the "hard sciences", where causal behavior can be reduced to fundamental well-founded primitives. Examples of symbology used to express FOL are the truth tables and logic gate representations in electronics. Symbols used in these schematics provide clear documentation of, not only the constituents of a circuit, but a picture of the operation of that circuit. A difficulty called the "completeness" problem exerts itself: to perform system-level analyses, one must model some critical mass of the system being studied. Electronic engineers constantly grapple with this problem because the symbology used to describe complex digital circuits cannot provide an adequate picture of their operation – the story of their miniature worlds are difficult to tell. Engineers are now being asked to develop hardware in a manner that is similar to high-level languages used to develop software. An article featured in EDD August 4, 1994 states the problem rather surprisingly:
"Unfortunately, a textual source listing of HDL (hardware description language) code doesn't provide all the information contained in a schematic's graphics. Although some of the graphical information is available--you have to provide names of interface signals and the directions of signal flows when you define VHDL (very-high-speed integrated circuits) components--other information doesn't easily fit into the HDL process. Signal feedback, locality, and sequenced vs parallel operation, for example, have no explicit graphical representation in HDL code. The HDL-development process must recognize these deficiencies and provide a means of compensation. When experienced circuit designers are just becoming familiar with HDL-based design, they often express a feeling of discomfort with the process. However, after being shown methods that compensate for information loss, they realize that information loss was the source of their discomfort." [18]
|
The top image (a) is a symbolic logic representation of the circuit shown in (b). A schematic provides much more information than just showing how things connect. Graphic symbols--shown here in military (a) and ANSI (b) forms--show, among other things, component functionality. Useful information such as this in HDL-based design can be lost unless precautions are taken.
|
As can be seen, many processes in the real world do not fit neatly into well described cases. They fall into what is called the realm of "soft" or "fuzzy" logic.
The Case For "Fuzzy" Logic
Fuzzy logic was developed by Dr. Lofti Zadeh of the University of California, Berkeley, in the late 1960s as a means of representing concepts that cannot be defined precisely, but which depend upon their context. The term is generally used in association with computing, where numbers on a scale from 0 to 1 ("degrees of truth") are used instead of the absolute values of "true" and "false", to accurately represent the fact that some questions do not have a simple yes or no answer. This attribute allows computerized devices using fuzzy logic to reason more like humans. Dr. Zadeh's work on the problem of computer understanding of natural language, an activity that is not easily translated into 0's and 1's, is what led to the notion of fuzzy logic.
Fuzzy logic includes 0 and 1 as extreme cases of truth ("the state of matters" or "fact") but also includes the various states of truth in between. This allows the result of comparison between two things to be not "black" or "white" but ".45 of whiteness." Fuzzy logic simulates the way biologically-based brains work. We gather data to form partial truths ("the lion seems to be coming in my direction") which we aggregate into higher truths ("a lion within striking distance is not a good thing") which in turn, cause us to act when certain thresholds are exceeded ("the lion is too close... run!"). These kinds of processes are used in artificial intelligence, expert systems, and neural networks.
The logic (fuzzy or otherwise) of a complex situation is rarely easy to visualize. Numbers, words, and symbols can be used to provide only a partial view into what is often a dynamic event, or series of events. The Kabbalah lends some insight into how such a notation can be attempted. Consider that the basic hermetic unit, the triad, consists of two circles representing fact or a functional entity. Connecting them is a line, which represents a relation between them. We do not know the quality of that relationship, that is to say, we cannot tell if information is exchanged, or if one entity effects the state of the other, but we do know there is a functional relationship between them. A third circle represents the "situation", or the result of the interaction between two entities. Thus, there are three recognizable aspects of this system: entities, functions between them, and the situation that there exists entities that are functionally related. Harriot created a system of notation using paths and circles associated with the Chablis symbols which allowed him to convey both the statement of equations between them, and the general situation of the equation. Unfortunately, the system Harriot developed was too cumbersome to be useful, but it did lead others to realize that logic biased against "situational" representations was missing something.
Peirce's study of pragmatics[19] in 1852 led to his conclusion that a "thirdness" was essential to a well-founded system of logic. "Thirdness" was restored to logic in the 1980s when Barwise and Perry[20] introduced the concept of a "situation" as a first class object in logic. They proposed that a situation is a simple entity which can carry context and attitude. The power of a situation is that it can act as a placeholder for information which is necessary to an analysis, but which is not easily expressed as "hard" facts. This has lead the way to a new soft logic referred to by "Situational Theory" – one which may provide insights [21] into the way the mind works.
The Case For "Fuzzy" Logic
Fuzzy logic was developed by Dr. Lofti Zadeh of the University of California, Berkeley, in the late 1960s as a means of representing concepts that cannot be defined precisely, but which depend upon their context. The term is generally used in association with computing, where numbers on a scale from 0 to 1 ("degrees of truth") are used instead of the absolute values of "true" and "false", to accurately represent the fact that some questions do not have a simple yes or no answer. This attribute allows computerized devices using fuzzy logic to reason more like humans. Dr. Zadeh's work on the problem of computer understanding of natural language, an activity that is not easily translated into 0's and 1's, is what led to the notion of fuzzy logic.
Fuzzy logic includes 0 and 1 as extreme cases of truth ("the state of matters" or "fact") but also includes the various states of truth in between. This allows the result of comparison between two things to be not "black" or "white" but ".45 of whiteness." Fuzzy logic simulates the way biologically-based brains work. We gather data to form partial truths ("the lion seems to be coming in my direction") which we aggregate into higher truths ("a lion within striking distance is not a good thing") which in turn, cause us to act when certain thresholds are exceeded ("the lion is too close... run!"). These kinds of processes are used in artificial intelligence, expert systems, and neural networks.
The logic (fuzzy or otherwise) of a complex situation is rarely easy to visualize. Numbers, words, and symbols can be used to provide only a partial view into what is often a dynamic event, or series of events. The Kabbalah lends some insight into how such a notation can be attempted. Consider that the basic hermetic unit, the triad, consists of two circles representing fact or a functional entity. Connecting them is a line, which represents a relation between them. We do not know the quality of that relationship, that is to say, we cannot tell if information is exchanged, or if one entity effects the state of the other, but we do know there is a functional relationship between them. A third circle represents the "situation", or the result of the interaction between two entities. Thus, there are three recognizable aspects of this system: entities, functions between them, and the situation that there exists entities that are functionally related. Harriot created a system of notation using paths and circles associated with the Chablis symbols which allowed him to convey both the statement of equations between them, and the general situation of the equation. Unfortunately, the system Harriot developed was too cumbersome to be useful, but it did lead others to realize that logic biased against "situational" representations was missing something.
Peirce's study of pragmatics[19] in 1852 led to his conclusion that a "thirdness" was essential to a well-founded system of logic. "Thirdness" was restored to logic in the 1980s when Barwise and Perry[20] introduced the concept of a "situation" as a first class object in logic. They proposed that a situation is a simple entity which can carry context and attitude. The power of a situation is that it can act as a placeholder for information which is necessary to an analysis, but which is not easily expressed as "hard" facts. This has lead the way to a new soft logic referred to by "Situational Theory" – one which may provide insights [21] into the way the mind works.
Neural Networks
A neural network is comprised of many simple processors that imitates a biological neural network. The term comes from mathematicians Warren McCulloh and Walter Pitts[22], who described the "neuro-logical" properties of connected neurons. They identified that neurons add quantities, compare sums to a threshold, and indicate whether the threshold is exceeded. Biologically things are a bit more complicated than that, but McCully and Pitts showed that individual neurons are configured to form logic gates which employ the principle of "degrees of truth" (or in this case, degrees of signal activity between neurons).
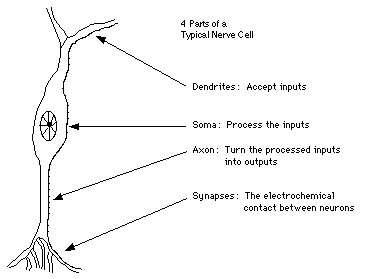
Natural neurons have four basic components: dendrites, soma, axon, and synapses. The figure below shows a simplified biological neuron and the relationship of its four components.
A neural network is comprised of many simple processors that imitates a biological neural network. The term comes from mathematicians Warren McCulloh and Walter Pitts[22], who described the "neuro-logical" properties of connected neurons. They identified that neurons add quantities, compare sums to a threshold, and indicate whether the threshold is exceeded. Biologically things are a bit more complicated than that, but McCully and Pitts showed that individual neurons are configured to form logic gates which employ the principle of "degrees of truth" (or in this case, degrees of signal activity between neurons).
Natural neurons have four basic components: dendrites, soma, axon, and synapses. The figure below shows a simplified biological neuron and the relationship of its four components.
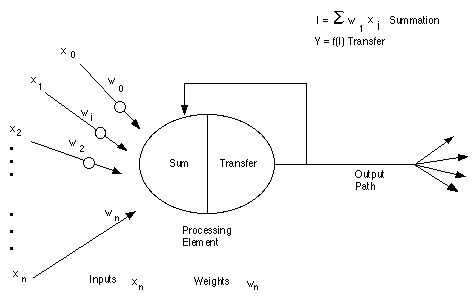
Basics of artificial neurons are shown in the figure below. Multiple inputs to the network are represented by the mathematical symbol, x(n). Each of these inputs are multiplied by a connection weight, which are represented by w(n). In simple cases, these products are summed, taken through a transfer function to generate a result, and then output.
The extraordinary connectivity between neurons in a brain (called everything-connected-to-everything connections) can be simulated in the hardware and software of digital computers. Networks so configured can represent degrees of facts, probabilities of events, and can make decisions based on statistical information. Such networks begin to resemble human thought processes. Psychologists and AI researchers use these networks to model examples of pattern recognition. Neural networks, sometimes called "auto-associators", exhibit five features: 1) Reconstructive, content addressable memory, 2) graceful degradation, 3) constraint satisfaction, 4) ability to generalize automatically, 5) learning from examples.[23]
Language and Mind
"I call language an 'instinct', an admittedly quaint term for what other cognitive scientists have called a mental organ, a faculty, or a module. Language is a complex, specialized skill, which develops in the child spontaneously without conscious effort or formal instruction, is deployed without awareness of its underlying logic, is qualitatively the same in every individual, and is distinct from more general abilities to process information or behave intelligently." -- Steven Pinker
Psycholinguistics, a hybrid discipline created from psychology and the linguistics, has only recently achieved the level of an accepted discipline, with its own theories, assumptions, and research method. This merging of studies into mental and behavioral operations with the study of language elements and structure has yielded some insight into the operation of the human mind -- at least as brain operation is related to language. Research in the psychology of language has played a major role in AI studies. It has contributed greatly in attempts to create computers that can process natural language and in the problems of how language is stored in memory in both the mind and in a computer.
Early stages of linguistics assumed the behaviorist approach, where linguists only analyzed behavior separate from mental operations. Phonetics (the sound of words) and semantics (structure and syntax) were the primary focus of linguistics. The relationship between psychology and language was forever linked by B.F. Skinner in 1957.[24] Skinner argued that the study of language required both a description of the types of verbal utterances and an explanation of their occurrence. He showed that psychological principles that apply for such attributes as human memory also explain the use of language and its acquisition.
Noam Chomsky went further by defining linguistics as a subdivision of cognitive psychology.[25] He argued that explanations of language at that time (1957) did not account for the information that native speakers of a language had at their disposal. Chomsky's claims about language have evolved over the years, however the major elements can be stated as follows:
Gilbert Ryle, a well-known figure in the "ordinary language" movement, reinforces the idea of mind as a set of mental organs. Ryle challenged the distinction between body and mind, stating that the mind is the form or organizing principle of the body.
Psycholinguistics came to an early distinction between surface and deep structures. The surface structure of a sentence is close to what is said and heard; similar to the sentence being performed ("Spot ran across the street"). Deep structure represents both the meaning elements and their relationships ("The street was ran by Spot"). This is the level of sentence structure that is thought to be the reason for a vast variety of language elements. Newer models theorize variously that:
The search for an adequate model for understanding the complex relationships between language and the mind have caused psycholinguists to lean in favor of a purely psychological model of language behavior. This is because empirical evidence indicated that a correspondence between the psychological theory (or model of language competence) and an identical linguistic model did not hold. The main issues confronting the psycholinguistic field are phonology, semantics, syntax, and an explanation of the acquisition of language.
Chomsky believes that there is no essential element of "language" that is external to the human mind. He argues that the study of language should focus on the mental construct that constitutes our knowledge of language.[27] According to Chomsky, children are born with a language-acquisition device that enables them to hear, analyze, and derive the rules of language from speech. Others have proposed that the language-acquisition device contains universals of human language (such as subject-predicate relationships). Many psycholinguists assume that basic information for dealing with language is essentially innate.
Pinker put the final touch on the language/mind connection:
"The mind, I claim, is not a single organ but a system of organs, which we can think of as psychological faculties or mental modules. The entities now commonly evoked to explain the mind—such as general intelligence, a capacity to form culture, and multipurpose learning strategies—will surely go the way of protoplasm in biology and of earth, air, fire, and water in physics. These entities are so formless, compared to the exacting phenomena they are meant to explain, that they must be granted near-magical powers. When the phenomena are put under a microscope, we discover that the complex texture of the everyday world is supported not by a single substance but by many layers of elaborate machinery."[28]
Color and The Mind
Color is essential in the world in which we live. Color can cause reactions, effect thinking, and change actions. Color is an irreplaceable and subliminal form of communication throughout all realms of life on our planet. Traffic lights universally show red to mean "stop" and green to mean "go."
Good use of color in design saves a viewer from thinking too much. Color perception is deeply wired into our brains because we have many millions of years of evolution to thank for it. As a result, color perception is rapid, accurate, and effortless for us. Reading text, attaching meaning to a symbol, searching memory for the answer — activities involved in thinking— is not something we are particularly good at by comparison, because these are evolutionarily newer features.
Color plays such an essential role in our interaction with the visual world that we automatically deal with it using what is known as "preattentive" and "attentive" processing. This allows for a divide and conquer strategy, where we decompose the image into pieces that are examined one at a time. Preattentive processing occurs when a viewer first encounters an image. At this stage the viewer has not focused attention on any particular location or object. Nothing is processed yet for meaning, however, the image is divided into chunks for the attentional processing stage. The attentive stage, as its name suggests, is when we intentionally focus on objects that are then processed for meaning (what the symbols mean) and are no longer simply patches of color. We move the eyes so that the area of importance forms an image on the fovea, the highest acuity area of the retina.
There are other, more subtle aspects of the process that come into play. The important thing as far as color and the mind goes, is that we derive meaning, context, and relevance from the visual world because we've been "wired" to do so. Our perception of things is intimately related to their meaning, at least on a very quickly processed "primitive" level. This point is paramount to good graphic design. The mind categorizes so quickly and efficiently that the attentional system can be used to indicate parts of an image which form distinct areas and, if the same color is found in different parts of an image, link those areas together as having something in common. This ability of the mind to quickly process visual images, and information to be derived from them, can be easily thwarted. The mind tells us that oranges are not blue, that vertical and horizontal lines are different things, and that we can expect to see the horizon below us. Confusion occurs when things are "not right".
Similar colors suggests relationships between objects and areas of an image. The ability to form associations through color is built into us. Significantly, there is no limit to this capacity, so we can see these relationships over the entire image at once. When confronted with color-coded data the eyes make a rapid movement called a saccade to all related areas of the image. Color short-cuts allows people to bypass irrelevant parts of an image and direct attention to related parts.[29]
Co-Evolutionary Convergence
In philosophy, universals are general terms or abstract concepts, of which there may be particular individual instances. For example, red is a universal, of which the red square is an instance. Universals are considered essential to thought and language, but differing views exist as to their origin and nature of existence.[30] Terrence W. Deacon argues that the source of universal rules regarding language and color have emerged spontaneously and independently in all evolving groups of people distinguished by language. The universals exist as a response to biases in the selection process affecting language transmission in cultures. Such universals are, therefore, a convergent feature of language evolution in the same way that the strong hind legs of cats, deer, and kangaroos are independent adaptations of mammals. Deacon sites convergent word references for color as an example of this co-evolutionary convergence process.[31]
Perceptual experiences about color is different for all individuals ("Do you see the same red that I see"?). However, the mappings of color terms to light frequencies are nearly universal in the world's languages. Although different cultures possess different words and color naming conventions, Berlin and Kay[32] found that everyone organizes color the same way. They found, in a series of cross-cultural comparisons, a regularity in terms for different colors in different societies. Other studies show that when given color samples and simply asked to organize them into piles based on "similarity," people in all cultures group the samples into the same color-differentiated piles. This, however, does not apply to emotional or cultural meanings attached to colors among societies. For example, white is associated with death and mourning in Eastern cultures, where black is associated with the same meanings in the West.
Deacon concludes his point about the universality of color perception as follows:
"In many ways, primary color term reference relationships are as invariant and universal in character as is any aspect of the deep logic of human grammars, and yet it is clear that color terms themselves are not built into the brain, and that choice of what color to designate with a particular word is not dictated by any mental compulsion. What is universally built into the brain is a rather subtle set of perceptual biases that have none of the categorical and symbolic properties of words."[33]
Color: Meaning and Use
Color can create strong associations when presented with specific shapes and locations. The brand name "Pepto-Bismol" conjures not only the product, but a specific shade of pink. The National Geographic yellow is instantly recognizable, along with the smaller shape of the magazine. Although an extremely powerful component of visual communication, color can be challenging to work without careful and self-consistent use in design. The need grows for clear concise information systems to keep pace with the amount of information we are increasingly confronted with. Methodologies for automatically communicating in graphics - selection of appropriate colors, shapes, mapping data, and color coding—using somewhat universal techniques, may be developed in the future.
Meaning
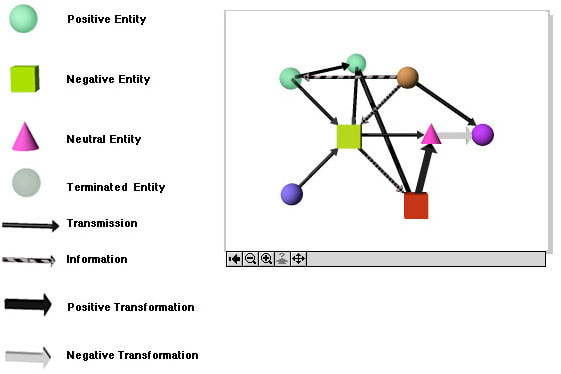
Color is universally used to convey specific meanings such as warning (red), caution (yellow), safety (green), and so on. The OSHA (Occupational Safety and Health Agency) has standardized the following color codes:
red - danger
orange - warning
yellow - caution
blue - notice
green - safety
A somewhat feeble attempt in the computer field to standardize has emerged for data entry fields:
gray field - read only data
white field - optional data entry field
yellow field - required data entry field
red field - error in field entry
The main challenge with standardization of colors is that the form must follow function and context. The function of colors cannot be placed into a tidy conceptual box which can contain those things "...that have none of the categorical and symbolic properties of words." In the real, (non man-made) world the color of objects is determined by a host of evolutionary, biological, chemical, and physical factors. The way we deal with, and interpret the colors of the earth, fauna, and wildlife around us on a forest trail is very different from the way we interpret colors on a map meant to represent that location. We are not doing much abstract thinking when the more immediate and primitive parts of our brain is trying to determine if a bear is moving in our direction. The contrast between brown and green then occupies our full "preattentive" and "attentive" faculties, notwithstanding the "meaning" attached to the color brown at that moment.
Use of Color
Effective design of knowledge systems using elements of color should incorporate certain well-defined principles. Senders and Green[34] offer the following advice:
Approaches to Descrete Event Simulation
The term "Descrete Event Simulation" is the consequence of nearly fifty years of research into problem-solving techniques.[39] Modeling methodology, which defines a theory of models and the modeling process and their relation to decision-making, is an integral part of simulation. Much of this work is involved in the areas of time flow, conceptual frameworks, simulation programming languages, and modeling life cycles, but it has suffered from a lack of standard terminology. Nance[40] lamented a "common language of discourse" and proposed a set of definitions based on the fundamental relationship between time and state in descrete event simulation.
Central to any useful simulation is its ability to model a system. An adaptation of the definition for system contained in the Delta project report is as follows:
"A system is a part of the world which we choose to regard as a whole, separated from the rest of the world for some period of consideration, a whole which we choose to consider as containing a collection of components, each characterized by a selected set of data items and patterns, and by actions which may involve itself [a component] and other components."[41]
The system may not necessarily be real, and may receive input from, and/or produce output for, any environment it is a part of.
A model is an abstraction of a system intended to replicate some properties of that system.[42] It is essential that the modeling objective must be included in the collection of properties the model is intended to represent. Therefore, model assumptions must be reconciled with the modeling objective in order to provide meaning to the simulation elements.
Nance[43] posits that a model is comprised of objects and the relationships among objects. An object is anything distinguished by one or more attributes to which values are assigned. Note that the concept of a "situation" introduced by Barwise and Perry (1983) for logic is similar to Nance's term "state". Nance identifies the following primitives which allow for delineation of the relationship between the fundamental concepts of time and state:
These definitions yield simulation concepts in wide use today:
Methods of representing models are varied, and often do not show the only description of a system. It is important to note that methods for modeling have been used long before, and in conjunction with the advent of the digital computer. As noted earlier, systems of notating events and their meanings have been developed over hundreds of years. According to Page[44] , "... any method of description must contain a set of attributes whose value changes describe the lifetime of the model. And an object-based description would seem to provide the best available means of organizing these attributes."
Modeling and Simulation
In management science models of situations being analyzed have been used for many years. The model is typically a simplified representation of a system intended to explain some aspect of it. Linear programming (mathematical programming), where the model is an abstract mathematical formulation of the problem, is a well-known technique. Of course, simulation models are also used for testing everything from the performance of an traffic control systems to how people stand in line waiting for hamburgers. Central to the use of models is the ability of the modeling system to be used for conceptualization, representation, analyzing, and implementation. The following paragraphs describe some of the techniques used to represent descrete event simulations.
Lackner's General Theory of Systems
The early days of computer simulation were dominated by the use of simulation program language (SPL) development. Michael Lackner recognized the need to develop a general theory of systems and models that are separate from SPLs. Lackner stated[45] :
"What has happened in the development of simulation languages is this: the orderly scheme of relationships has been expressed in computer code, the programs that are a part of every model. A modeler using the language understands that this scheme is supplied; he does not alter the scheme in using the language; he describes system elements in accordance with the category system, which is also invariant. The simulation language is a part of a simulation scheme that is based on a theory of systems, but the theory has been neither elucidated nor developed. ...Only by appeal to this [general] theory [of systems] may a modeler say ``this is a model of object system x'' and ``this is how the model behaves.'' Only by such appeal may he explain why it is a model, and why the model so behaves. ... Furthermore, development of system theory should make possible deductions of interesting measures and properties of simulation models that are not dependent on empirical observation of the models' [sic.] behavior."
Lackner presented a theory of discrete event systems in which change, not time, is primitive - and that time is defined in terms of change. His findings are summarized in the following paragraphs.[46]
He observed that the fundamental dilemma faced in simulation modeling is the necessity of representing the dynamic in terms of the static. Whatever methods are used, limitations are bound to be encountered. The logical usefulness (and complexity) of the model may be improved by adding conditional procedures, but many systems still lack in the program structure: 1) the asynchronous operation of related components, and (2) the effects of varying duration of independent processes. These system characteristics are among the most difficult to reduce to mathematical expression. Here we are reminded of Harriot's system of notation which lead others to realize that logic biased against "situational" representations was missing something.
Several approaches and methodologies (including Lackner's calculus) for discrete event modeling trace their origins to general systems theory. General systems theory states that real systems obey the same laws and show similar patterns of behavior even if they are physically different.[47]
Activity Cycle Diagrams
Tocher[48] introduced a notation for describing the logical "flow" of a situation and represent one of the earliest attempts to provide a graphical description of a simulation model. They are, however flowcharts in the classic sense. Further development of the notation into what is called "wheel charts" was possibly inspired by this fact. Wheel chart notation was further evolved into a form known as activity cycle diagrams (or entity cycle diagrams) first described in 1960.
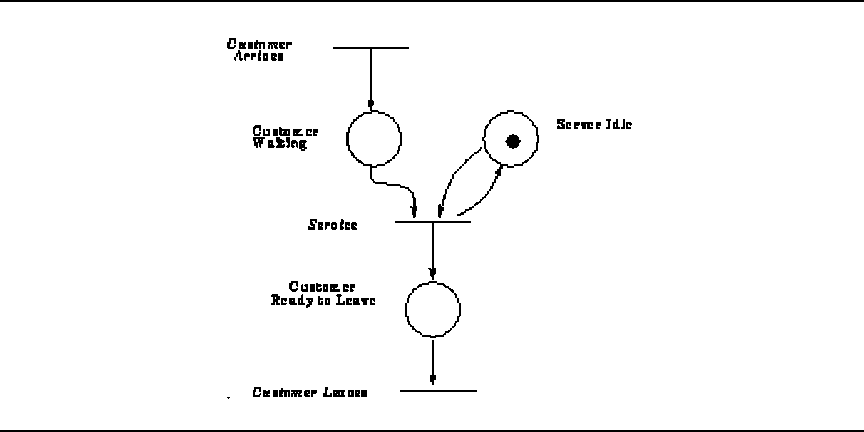
In the typical activity cycle diagram (ACD), the simulation model is viewed as a collection of interacting entities. An entity is any component of the model which retains its identity through time. Entities are either idle (in notional or real queues), or active (engaged with other entities in activities that take place over time). An active state generally involves the cooperation of, or interaction between, different entities. A passive state (queueing state), involves no cooperation between different entities and is generally a state in which the entity waits for something to happen. The duration of an activity is always determined in advance, whereas the duration of the queueing state cannot be determined.[49] The symbology for ACDs is minimal, with one symbol each for a queue and an activity.
To specify a model using ACDs, an activity cycle (or life cycle), composed of queues and activities must be provided for each class of entity in the model. A fault is that queues and activities must alternate in the representation, consequently dummy queues are incorporated into the diagram. Typically each activity cycle must be closed.
Event-Oriented Graphical Techniques
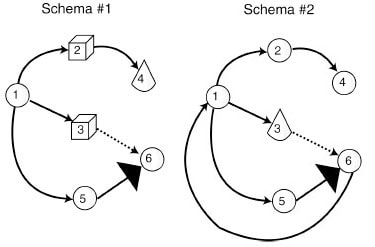
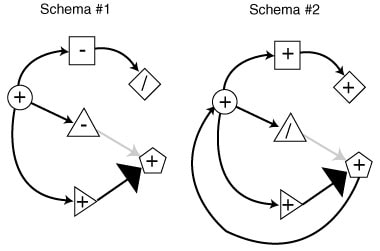
Observing that graphical modeling techniques had been developed for discrete event simulations adopting either an activity scan (activity cycle diagrams) or process interaction (GPSS block diagrams) view, but that no such tool was available for event scheduling models, Schruben introduces a formalism dubbed the event graph. Using Schruben's terminology, the crucial elements of a discrete event simulation are state variables that describe the state of the system, events that alter the values of state variables, and the logical and temporal relationships among events. An event graph is a directed graph that depicts the interrelation of the events in an event scheduling discrete event simulation. To construct an event graph, events are defined and numbered, and represented as vertices in the digraph. Event vertices are connected by directed edges that indicate how one event influences the occurrence of another event. Two classes of edges are defined: a solid edge represents the scheduling of an event; a dashed edge represents an event cancellation.
Petri Net Method
A Petri net (named for Carl Petri), is an abstract formal model of information flow, used to model systems which exhibit concurrency. This method has been suggested as a formalism to model general systems for discrete event simulation. Petri nets are appropriate for modeling systems that can be viewed as a set of events and a set of conditions, and the relationships among these sets.
A Petri net is a graph which contains two types of nodes: places (usually represented by circles), and transitions (usually represented by bars). An arc drawn in the graph may exist only between places and transitions - multiple arcs between any two nodes are not allowed. If an arc is drawn from a (P)lace to a (T)ransition, then P is termed an "input place of transition T", and T is termed an "output transition of place P". Similar definitions hold for output place and input transition.
"I call language an 'instinct', an admittedly quaint term for what other cognitive scientists have called a mental organ, a faculty, or a module. Language is a complex, specialized skill, which develops in the child spontaneously without conscious effort or formal instruction, is deployed without awareness of its underlying logic, is qualitatively the same in every individual, and is distinct from more general abilities to process information or behave intelligently." -- Steven Pinker
Psycholinguistics, a hybrid discipline created from psychology and the linguistics, has only recently achieved the level of an accepted discipline, with its own theories, assumptions, and research method. This merging of studies into mental and behavioral operations with the study of language elements and structure has yielded some insight into the operation of the human mind -- at least as brain operation is related to language. Research in the psychology of language has played a major role in AI studies. It has contributed greatly in attempts to create computers that can process natural language and in the problems of how language is stored in memory in both the mind and in a computer.
Early stages of linguistics assumed the behaviorist approach, where linguists only analyzed behavior separate from mental operations. Phonetics (the sound of words) and semantics (structure and syntax) were the primary focus of linguistics. The relationship between psychology and language was forever linked by B.F. Skinner in 1957.[24] Skinner argued that the study of language required both a description of the types of verbal utterances and an explanation of their occurrence. He showed that psychological principles that apply for such attributes as human memory also explain the use of language and its acquisition.
Noam Chomsky went further by defining linguistics as a subdivision of cognitive psychology.[25] He argued that explanations of language at that time (1957) did not account for the information that native speakers of a language had at their disposal. Chomsky's claims about language have evolved over the years, however the major elements can be stated as follows:
- The ordinary use of language is creative.
- There is a fundamental distinction between behavior and knowledge, and that knowledge is the proper focus of scientific study.
- Representation of a speaker's linguistic knowledge requires affirming the existence of a set of abstract principles, the discovery of which by individuals suggests a complex biological component to language acquisition.
- These principles, which Chomsky referred to as "universal grammar" are specific to our facility with language.
- The principles contribute to a notion of the mind as a set of mental organs, including language.
Gilbert Ryle, a well-known figure in the "ordinary language" movement, reinforces the idea of mind as a set of mental organs. Ryle challenged the distinction between body and mind, stating that the mind is the form or organizing principle of the body.
Psycholinguistics came to an early distinction between surface and deep structures. The surface structure of a sentence is close to what is said and heard; similar to the sentence being performed ("Spot ran across the street"). Deep structure represents both the meaning elements and their relationships ("The street was ran by Spot"). This is the level of sentence structure that is thought to be the reason for a vast variety of language elements. Newer models theorize variously that:
- Surface and deep structures may be closer in meaning than previously thought
- More levels of structure may be involved in language processing
- Other factors, such as the context in which a sentence is communicated, may be more important to meaning than structures
- Deep and surface structures may simply be theoretical constructs with no basis in reality.[26]
The search for an adequate model for understanding the complex relationships between language and the mind have caused psycholinguists to lean in favor of a purely psychological model of language behavior. This is because empirical evidence indicated that a correspondence between the psychological theory (or model of language competence) and an identical linguistic model did not hold. The main issues confronting the psycholinguistic field are phonology, semantics, syntax, and an explanation of the acquisition of language.
Chomsky believes that there is no essential element of "language" that is external to the human mind. He argues that the study of language should focus on the mental construct that constitutes our knowledge of language.[27] According to Chomsky, children are born with a language-acquisition device that enables them to hear, analyze, and derive the rules of language from speech. Others have proposed that the language-acquisition device contains universals of human language (such as subject-predicate relationships). Many psycholinguists assume that basic information for dealing with language is essentially innate.
Pinker put the final touch on the language/mind connection:
"The mind, I claim, is not a single organ but a system of organs, which we can think of as psychological faculties or mental modules. The entities now commonly evoked to explain the mind—such as general intelligence, a capacity to form culture, and multipurpose learning strategies—will surely go the way of protoplasm in biology and of earth, air, fire, and water in physics. These entities are so formless, compared to the exacting phenomena they are meant to explain, that they must be granted near-magical powers. When the phenomena are put under a microscope, we discover that the complex texture of the everyday world is supported not by a single substance but by many layers of elaborate machinery."[28]
Color and The Mind
Color is essential in the world in which we live. Color can cause reactions, effect thinking, and change actions. Color is an irreplaceable and subliminal form of communication throughout all realms of life on our planet. Traffic lights universally show red to mean "stop" and green to mean "go."
Good use of color in design saves a viewer from thinking too much. Color perception is deeply wired into our brains because we have many millions of years of evolution to thank for it. As a result, color perception is rapid, accurate, and effortless for us. Reading text, attaching meaning to a symbol, searching memory for the answer — activities involved in thinking— is not something we are particularly good at by comparison, because these are evolutionarily newer features.
Color plays such an essential role in our interaction with the visual world that we automatically deal with it using what is known as "preattentive" and "attentive" processing. This allows for a divide and conquer strategy, where we decompose the image into pieces that are examined one at a time. Preattentive processing occurs when a viewer first encounters an image. At this stage the viewer has not focused attention on any particular location or object. Nothing is processed yet for meaning, however, the image is divided into chunks for the attentional processing stage. The attentive stage, as its name suggests, is when we intentionally focus on objects that are then processed for meaning (what the symbols mean) and are no longer simply patches of color. We move the eyes so that the area of importance forms an image on the fovea, the highest acuity area of the retina.
There are other, more subtle aspects of the process that come into play. The important thing as far as color and the mind goes, is that we derive meaning, context, and relevance from the visual world because we've been "wired" to do so. Our perception of things is intimately related to their meaning, at least on a very quickly processed "primitive" level. This point is paramount to good graphic design. The mind categorizes so quickly and efficiently that the attentional system can be used to indicate parts of an image which form distinct areas and, if the same color is found in different parts of an image, link those areas together as having something in common. This ability of the mind to quickly process visual images, and information to be derived from them, can be easily thwarted. The mind tells us that oranges are not blue, that vertical and horizontal lines are different things, and that we can expect to see the horizon below us. Confusion occurs when things are "not right".
Similar colors suggests relationships between objects and areas of an image. The ability to form associations through color is built into us. Significantly, there is no limit to this capacity, so we can see these relationships over the entire image at once. When confronted with color-coded data the eyes make a rapid movement called a saccade to all related areas of the image. Color short-cuts allows people to bypass irrelevant parts of an image and direct attention to related parts.[29]
Co-Evolutionary Convergence
In philosophy, universals are general terms or abstract concepts, of which there may be particular individual instances. For example, red is a universal, of which the red square is an instance. Universals are considered essential to thought and language, but differing views exist as to their origin and nature of existence.[30] Terrence W. Deacon argues that the source of universal rules regarding language and color have emerged spontaneously and independently in all evolving groups of people distinguished by language. The universals exist as a response to biases in the selection process affecting language transmission in cultures. Such universals are, therefore, a convergent feature of language evolution in the same way that the strong hind legs of cats, deer, and kangaroos are independent adaptations of mammals. Deacon sites convergent word references for color as an example of this co-evolutionary convergence process.[31]
Perceptual experiences about color is different for all individuals ("Do you see the same red that I see"?). However, the mappings of color terms to light frequencies are nearly universal in the world's languages. Although different cultures possess different words and color naming conventions, Berlin and Kay[32] found that everyone organizes color the same way. They found, in a series of cross-cultural comparisons, a regularity in terms for different colors in different societies. Other studies show that when given color samples and simply asked to organize them into piles based on "similarity," people in all cultures group the samples into the same color-differentiated piles. This, however, does not apply to emotional or cultural meanings attached to colors among societies. For example, white is associated with death and mourning in Eastern cultures, where black is associated with the same meanings in the West.
Deacon concludes his point about the universality of color perception as follows:
"In many ways, primary color term reference relationships are as invariant and universal in character as is any aspect of the deep logic of human grammars, and yet it is clear that color terms themselves are not built into the brain, and that choice of what color to designate with a particular word is not dictated by any mental compulsion. What is universally built into the brain is a rather subtle set of perceptual biases that have none of the categorical and symbolic properties of words."[33]
Color: Meaning and Use
Color can create strong associations when presented with specific shapes and locations. The brand name "Pepto-Bismol" conjures not only the product, but a specific shade of pink. The National Geographic yellow is instantly recognizable, along with the smaller shape of the magazine. Although an extremely powerful component of visual communication, color can be challenging to work without careful and self-consistent use in design. The need grows for clear concise information systems to keep pace with the amount of information we are increasingly confronted with. Methodologies for automatically communicating in graphics - selection of appropriate colors, shapes, mapping data, and color coding—using somewhat universal techniques, may be developed in the future.
Meaning
Color is universally used to convey specific meanings such as warning (red), caution (yellow), safety (green), and so on. The OSHA (Occupational Safety and Health Agency) has standardized the following color codes:
red - danger
orange - warning
yellow - caution
blue - notice
green - safety
A somewhat feeble attempt in the computer field to standardize has emerged for data entry fields:
gray field - read only data
white field - optional data entry field
yellow field - required data entry field
red field - error in field entry
The main challenge with standardization of colors is that the form must follow function and context. The function of colors cannot be placed into a tidy conceptual box which can contain those things "...that have none of the categorical and symbolic properties of words." In the real, (non man-made) world the color of objects is determined by a host of evolutionary, biological, chemical, and physical factors. The way we deal with, and interpret the colors of the earth, fauna, and wildlife around us on a forest trail is very different from the way we interpret colors on a map meant to represent that location. We are not doing much abstract thinking when the more immediate and primitive parts of our brain is trying to determine if a bear is moving in our direction. The contrast between brown and green then occupies our full "preattentive" and "attentive" faculties, notwithstanding the "meaning" attached to the color brown at that moment.
Use of Color
Effective design of knowledge systems using elements of color should incorporate certain well-defined principles. Senders and Green[34] offer the following advice:
- Use hue to show categorical distinctions. Code categorical variables such as country, individual, etc. with color but not quantitative variables such as amount of money, weight, etc. However, there are exceptions:
- It is sometimes useful to break continuous variables into categories to aid interpretation. A monitoring system might quantize the continuous variable temperature in categories safe (green), caution (yellow) and warning (red) or a system might use color to differentiate positive and negative numbers while using brightness to quantify with each class.
- If the user has a control for thresholding, then use hue to quantize continuous variables. For example, if the user is looking at a brain scan, then provide a control for thresholding some cell function (metabolic activity, etc.) to different levels. Make all brain areas above the threshold one hue and all below a different hue.
- If drawing a graph with thin lines or very small data points, remember that the eye does not discriminate colors of small objects very well. Don’t expect people to easily discriminate data represented in blue from data represented in black or yellow from white. Use larger data points and/or more discriminable, high saturation colors for important distinctions.
- If using small data points, employ high brightness contrast. The viewer will have difficulty discriminating the difference between data points, such as small squares and circles, unless there is high achromatic contrast. Remember that the chromatic system has poor spatial resolution, so color contrast won’t help discriminate small shapes. Similarly, if there are dotted lines, make sure that the dots are discriminable from the background.
- Use standard color meanings if possible. Heat is red, money is green, etc. However, don’t rely on color solely and don’t assume that the viewer will understand. Back up the color meanings with a legend.
- If the viewer is expected to remember a specific meaning for each color (a different year, person, industry, etc.) from one graph or chart to the next, use no more than 5 colors. Each should be central category member.
- Use high color contrast and saturation to show emphasis and to draw attention to important information. Conversely, use low contrast to indicate secondary importance
- Optimize use of preattentive processing. The importance of optimizing preattentive processing and of minimizing thinking has been widely acknowledged in the visualization literature. Cleveland (1984)[35] , for example, has noted that in "elementary graphical-perception tasks," the preattentive perception of basic graphical elements underlies data visualization. Abarbanel (1993)[36] suggested that visualization can be defined as the substitution of "preconscious visual competencies" for "conscious thinking." Woods (1991)[37] further said that "If the mental activities required to locate base data units are not automatic, but require mental effort or capacity, they may disrupt or divert...the main line of reasoning." The terms, "preattentive," "immediate," "preconscious" and "automatic" all highlight the necessity of designing displays so that the viewer can effortlessly perceive the fundamental visual element and distinctions. See our article "Toward a Perceptual Science of Multidimensional Data Visualization: Bertin and Beyond".[38]
Approaches to Descrete Event Simulation
The term "Descrete Event Simulation" is the consequence of nearly fifty years of research into problem-solving techniques.[39] Modeling methodology, which defines a theory of models and the modeling process and their relation to decision-making, is an integral part of simulation. Much of this work is involved in the areas of time flow, conceptual frameworks, simulation programming languages, and modeling life cycles, but it has suffered from a lack of standard terminology. Nance[40] lamented a "common language of discourse" and proposed a set of definitions based on the fundamental relationship between time and state in descrete event simulation.
Central to any useful simulation is its ability to model a system. An adaptation of the definition for system contained in the Delta project report is as follows:
"A system is a part of the world which we choose to regard as a whole, separated from the rest of the world for some period of consideration, a whole which we choose to consider as containing a collection of components, each characterized by a selected set of data items and patterns, and by actions which may involve itself [a component] and other components."[41]
The system may not necessarily be real, and may receive input from, and/or produce output for, any environment it is a part of.
A model is an abstraction of a system intended to replicate some properties of that system.[42] It is essential that the modeling objective must be included in the collection of properties the model is intended to represent. Therefore, model assumptions must be reconciled with the modeling objective in order to provide meaning to the simulation elements.
Nance[43] posits that a model is comprised of objects and the relationships among objects. An object is anything distinguished by one or more attributes to which values are assigned. Note that the concept of a "situation" introduced by Barwise and Perry (1983) for logic is similar to Nance's term "state". Nance identifies the following primitives which allow for delineation of the relationship between the fundamental concepts of time and state:
- An instant is a value of system time at which the value of at least one attribute of an object can be altered.
- An interval is the duration between two successive instants.
- A span is the contiguous succession of one or more intervals.
- The state of an object is the enumeration of all attribute values of that object at a particular instant.
These definitions yield simulation concepts in wide use today:
- An activity is the state of an object over an interval.
- An event is a change in an object state, occurring at an instant, and initiates an activity precluded prior to that instant. An event is said to be determined if the only condition on event occurrence can be expressed strictly as a function of time. Otherwise, the event is contingent.
- An object activity is the state of an object between two events describing successive state changes for that object.
- A process is the succession of states of an object over a span (or the contiguous succession of one or more activities).
Methods of representing models are varied, and often do not show the only description of a system. It is important to note that methods for modeling have been used long before, and in conjunction with the advent of the digital computer. As noted earlier, systems of notating events and their meanings have been developed over hundreds of years. According to Page[44] , "... any method of description must contain a set of attributes whose value changes describe the lifetime of the model. And an object-based description would seem to provide the best available means of organizing these attributes."
Modeling and Simulation
In management science models of situations being analyzed have been used for many years. The model is typically a simplified representation of a system intended to explain some aspect of it. Linear programming (mathematical programming), where the model is an abstract mathematical formulation of the problem, is a well-known technique. Of course, simulation models are also used for testing everything from the performance of an traffic control systems to how people stand in line waiting for hamburgers. Central to the use of models is the ability of the modeling system to be used for conceptualization, representation, analyzing, and implementation. The following paragraphs describe some of the techniques used to represent descrete event simulations.
Lackner's General Theory of Systems
The early days of computer simulation were dominated by the use of simulation program language (SPL) development. Michael Lackner recognized the need to develop a general theory of systems and models that are separate from SPLs. Lackner stated[45] :
"What has happened in the development of simulation languages is this: the orderly scheme of relationships has been expressed in computer code, the programs that are a part of every model. A modeler using the language understands that this scheme is supplied; he does not alter the scheme in using the language; he describes system elements in accordance with the category system, which is also invariant. The simulation language is a part of a simulation scheme that is based on a theory of systems, but the theory has been neither elucidated nor developed. ...Only by appeal to this [general] theory [of systems] may a modeler say ``this is a model of object system x'' and ``this is how the model behaves.'' Only by such appeal may he explain why it is a model, and why the model so behaves. ... Furthermore, development of system theory should make possible deductions of interesting measures and properties of simulation models that are not dependent on empirical observation of the models' [sic.] behavior."
Lackner presented a theory of discrete event systems in which change, not time, is primitive - and that time is defined in terms of change. His findings are summarized in the following paragraphs.[46]
He observed that the fundamental dilemma faced in simulation modeling is the necessity of representing the dynamic in terms of the static. Whatever methods are used, limitations are bound to be encountered. The logical usefulness (and complexity) of the model may be improved by adding conditional procedures, but many systems still lack in the program structure: 1) the asynchronous operation of related components, and (2) the effects of varying duration of independent processes. These system characteristics are among the most difficult to reduce to mathematical expression. Here we are reminded of Harriot's system of notation which lead others to realize that logic biased against "situational" representations was missing something.
Several approaches and methodologies (including Lackner's calculus) for discrete event modeling trace their origins to general systems theory. General systems theory states that real systems obey the same laws and show similar patterns of behavior even if they are physically different.[47]
Activity Cycle Diagrams
Tocher[48] introduced a notation for describing the logical "flow" of a situation and represent one of the earliest attempts to provide a graphical description of a simulation model. They are, however flowcharts in the classic sense. Further development of the notation into what is called "wheel charts" was possibly inspired by this fact. Wheel chart notation was further evolved into a form known as activity cycle diagrams (or entity cycle diagrams) first described in 1960.
In the typical activity cycle diagram (ACD), the simulation model is viewed as a collection of interacting entities. An entity is any component of the model which retains its identity through time. Entities are either idle (in notional or real queues), or active (engaged with other entities in activities that take place over time). An active state generally involves the cooperation of, or interaction between, different entities. A passive state (queueing state), involves no cooperation between different entities and is generally a state in which the entity waits for something to happen. The duration of an activity is always determined in advance, whereas the duration of the queueing state cannot be determined.[49] The symbology for ACDs is minimal, with one symbol each for a queue and an activity.
To specify a model using ACDs, an activity cycle (or life cycle), composed of queues and activities must be provided for each class of entity in the model. A fault is that queues and activities must alternate in the representation, consequently dummy queues are incorporated into the diagram. Typically each activity cycle must be closed.
Event-Oriented Graphical Techniques
Observing that graphical modeling techniques had been developed for discrete event simulations adopting either an activity scan (activity cycle diagrams) or process interaction (GPSS block diagrams) view, but that no such tool was available for event scheduling models, Schruben introduces a formalism dubbed the event graph. Using Schruben's terminology, the crucial elements of a discrete event simulation are state variables that describe the state of the system, events that alter the values of state variables, and the logical and temporal relationships among events. An event graph is a directed graph that depicts the interrelation of the events in an event scheduling discrete event simulation. To construct an event graph, events are defined and numbered, and represented as vertices in the digraph. Event vertices are connected by directed edges that indicate how one event influences the occurrence of another event. Two classes of edges are defined: a solid edge represents the scheduling of an event; a dashed edge represents an event cancellation.
Petri Net Method
A Petri net (named for Carl Petri), is an abstract formal model of information flow, used to model systems which exhibit concurrency. This method has been suggested as a formalism to model general systems for discrete event simulation. Petri nets are appropriate for modeling systems that can be viewed as a set of events and a set of conditions, and the relationships among these sets.
A Petri net is a graph which contains two types of nodes: places (usually represented by circles), and transitions (usually represented by bars). An arc drawn in the graph may exist only between places and transitions - multiple arcs between any two nodes are not allowed. If an arc is drawn from a (P)lace to a (T)ransition, then P is termed an "input place of transition T", and T is termed an "output transition of place P". Similar definitions hold for output place and input transition.
A Petri Net describing customers waiting at a bar for service
At any time, a (P)lace may have a token, represented by black dots in place nodes. A Petri net with tokens is called a "marked" Petri net. The distribution of tokens to places in a marked Petri net is known as its marking. Petri nets are valuable because of their ability to model the hierarchy of a system. This allows an entire net to be represented by a single place or transition for modeling at another, more abstract level, or places and transitions may be expanded into subnets to show more detailed modeling. Petri graphs typically do not contain any information about the timing of events within a model, although timing notations can be added.
Control Flow Graphs
In 1990 Cota and Sargent [50, 51] introduced a mechanism called a control flow graph (CFG) as a conceptual tool for developing parallel simulation algorithms. A control flow graph is a directed representation of the behavior of a process, or class of processes, in a discrete event model. Each node in the CFG represents a possible state of the process (control state or synchronization point ) in which the process waits from some condition to become true or for some period of time to pass.
Processes described by CFGs communicate through what is known as message passing. Each process has a set of state variables, and sets of input /output channels across which it may send and receive messages. A process is said to be a predecessor of its input channels, and a successor of its output channels. Any number of channels may exist between two processes.
Flowcharts
A flowchart is a graphic description of the procedure to be followed in solving a given problem. Flowcharts are comprised of boxes of different shapes connected by arrows. Starting at the beginning (typically the top of a diagram) one follows the arrows from box to box to perform the steps described. The step of the process is written inside each box. The shape of a box indicates the kind of action it represents, such as control (a rhomboid), decision making (a diamond), and process (a box).
Flowcharts are used in the design and description of computer programs because they can show the underlying logic of a process. Flowcharts are also commonly used to represent overall view manufacturing processes.
The Memetic Connection
Definition
A contagious information pattern that replicates by infecting human minds and altering their behavior, causing them to propagate the pattern. (Coined by Richard Dawkins in his book, "The Selfish Gene", 1970) An information pattern becomes a meme when it causes someone to replicate it, or to repeat it to someone else. All knowledge that can be transmitted is memetic.
Memes are transmitted by replication (copied from host to host), they mutate as they are replicated, and they combine with other memes. Central to the concept of memes is that they exhibit evolutionary processes because they produce other memes, more powerful memes that adapt to better infest human hosts. Memes feature a number of characteristics that influence how well they proliferate:
Control Flow Graphs
In 1990 Cota and Sargent [50, 51] introduced a mechanism called a control flow graph (CFG) as a conceptual tool for developing parallel simulation algorithms. A control flow graph is a directed representation of the behavior of a process, or class of processes, in a discrete event model. Each node in the CFG represents a possible state of the process (control state or synchronization point ) in which the process waits from some condition to become true or for some period of time to pass.
Processes described by CFGs communicate through what is known as message passing. Each process has a set of state variables, and sets of input /output channels across which it may send and receive messages. A process is said to be a predecessor of its input channels, and a successor of its output channels. Any number of channels may exist between two processes.
Flowcharts
A flowchart is a graphic description of the procedure to be followed in solving a given problem. Flowcharts are comprised of boxes of different shapes connected by arrows. Starting at the beginning (typically the top of a diagram) one follows the arrows from box to box to perform the steps described. The step of the process is written inside each box. The shape of a box indicates the kind of action it represents, such as control (a rhomboid), decision making (a diamond), and process (a box).
Flowcharts are used in the design and description of computer programs because they can show the underlying logic of a process. Flowcharts are also commonly used to represent overall view manufacturing processes.
The Memetic Connection
Definition
A contagious information pattern that replicates by infecting human minds and altering their behavior, causing them to propagate the pattern. (Coined by Richard Dawkins in his book, "The Selfish Gene", 1970) An information pattern becomes a meme when it causes someone to replicate it, or to repeat it to someone else. All knowledge that can be transmitted is memetic.
Memes are transmitted by replication (copied from host to host), they mutate as they are replicated, and they combine with other memes. Central to the concept of memes is that they exhibit evolutionary processes because they produce other memes, more powerful memes that adapt to better infest human hosts. Memes feature a number of characteristics that influence how well they proliferate:
|
Infectiousness
|
How easily they spread from one person to another. Aspects of infectiousness include:
|
|
Memorability
|
How long the idea will stay with the carrier. Aspects of memorability include:
|
|
Immortality
|
The meme must outlive the people carrying it. Aspects of immortality include:
|
The most significant contribution of the field of memetics is that it has extended Darwinian evolution to human culture. It is therefore possible to view ideas that spread effectively as not necessarily "good" ones, but as possessing powerful "memes" that compell us to pay attention to them on a deeply engrained evolutionary level (food, fear, danger, sex, etc.).
A Memetics Lexicon
The field of memetics is so vast and varied, that the LMSL has "borrowed" from some of its key elements to create a subset language which describes the evolution of varied systems. Key elements include:
A Memetics Lexicon
The field of memetics is so vast and varied, that the LMSL has "borrowed" from some of its key elements to create a subset language which describes the evolution of varied systems. Key elements include:
|
Icon
|
A sign that informs by its physical resemblance or similarity with features of its referent. (Krippendorff)
|
|
Information
|
Information is the meaning of the representation of a fact (or of a message) for the receiver. (Hornung) Literally that which forms within, but more adequately: the equivalent of or the capacity of something to perform organizational work, the difference between two forms of organization or between two states of uncertainty before and after a message has been received, but also the degree to which one variable of a system depends on or is constrained by (see constraint) another. e.g., the DNA carries genetic information inasmuch as it organizes or controls the orderly growth of a living organism
|
|
Input
|
An event external to a system which modifies the system in any manner.
A variable at the boundary of an organism or machine through which information enters, the set of conditions, properties or states which effect a change in a systems behavior, the medium of exogenous control (see open system, output). (Krippendorff) |
|
Output
|
Any change produced in the surrounding by a system. (Umpleby)
|
|
Catalyst
|
A property, event or material substance that must be present to synthesize or produce some other property, event or material substance without becoming part of the result of the process.
|
|
Transformation
|
A set of transitions (Ashby) from the possible states of a system to their respective successors.
In whatever language a transformation is stated, it should spell out the set of operands or states to which the transformation applies (see domain) and the set of transforms which result from applying that transformation (see range). A mathematical function, e.g., y=f(x), is one form of transformation, a code, a transition matrix, a causal network, a Petri-graph and a set of rewrite rules are others. (Krippendorff) |
|
State
|
The state of a system at a given instant is the set of numerical values which its variables have at that instant. (Ashby, l960, p. l6) Any well defined condition or property which can be recognized if it occurs again (Ashby) (see recognition). States may be described in terms of the set of instantaneous values of all the variables of the system (Klir). States are mutually exclusive. Sequential machines occupy only one state at a time, others may have more than one (see computers). (Krippendorff)
|
|
Schema
|
A person's point of view on some set of issues which greatly determines the way he or she responds to them. (Arbib)
|
|
Self-Reproduction
|
When a unity produces another with a similar organization to its own, through a process that is coupled to the process of its own specifications. Only autopoietic systems can self-reproduce. (Maturana and Varela, 1979)
|
|
Language
|
A systematic way of arranging symbols, usually to express meaning. It may be a Natural Language like Chinese, English or Swahili that humans use to communicate with one another, or a Programming Language in which programs are written for a computer. (Arbib)
A combinatorial system for arranging characters into words and complex expressions subject to the constraints of a syntax, a logic and a semantics. A syntax rules out some combinations of characters as ungrammatical and designates the others as legitimate linguistic expressions. A logic orders the legitimate expressions implicationally and informationally. A semantics relates these expressions to the larger system of which a language is a part thus constraining the expressions according to what is appropriate in the non-linguistic context of a situation (the larger system). The combinatorial properties of a language are responsible for the chosen expressions to carry information relative to the expressions possible in a given context. The sharing of facilities to generate linguistic expressions (see generative) and the ability to make comparisons within the system of possible expression brings linguistic communication to a logical level higher than communication without language. (Krippendorff) |
|
Exchange
|
Two-way flow of values, commodities, information or people with a constraint on or rules for the amounts or proportions going either way. e.g., exchange rules of currency by a rate, reciprocal exchange of gifts or favors. (Krippendorff)
|
The relationship between computer programs and processes of the human mind has been well established. Connections between them are inescapable, as insights gained by researchers in both fields (computer science and human psychology) now fuel each other. Note that in the lexicon presented above, there are numerous words normally associated with computer terms. David Dawkins draws a clear line between human mind viruses (meme) and computer viruses:
"Progressive evolution of more effective mind-parasites will have two aspects. New 'mutants' (either random or designed by humans) that are better at spreading will become more numerous. And there will be a ganging up of ideas that flourish in one another's presence, ideas that mutually support one another just as genes do and as I have speculated computer viruses may one day do. We expect that replicators will go around together from brain to brain in mutually compatible gangs. These gangs will come to constitute a package, which may be sufficiently stable to deserve a collective name such as Roman Catholicism or Voodoo. It doesn't too much matter whether we analogize the whole package to a single virus, to each one of the component parts to a single virus. The analogy is not that precise anyway, just as the distinction between a computer virus and a computer worm is nothing to get worked up about. What matters is that minds are friendly environments to parasitic, self-replicating ideas or information, and that minds are typically massively infected." [52]
The Need for a Universal Symbolic Language
Jump ahead 400 years to a time when humans are in intimate contact with alien races. The Star Trek universe is populated by starships of infinite variety with advanced technologies. A visit to Deep Space Nine, a space station outpost orbiting the planet Bajor near a stable wormwhole, places you bodily into the heart of Cardassian design. Control panels everywhere show a plethora of colorful symbols and animated displays. Amazingly, personnel working at displays in the Operations Center can monitor the smallest detail of the space station's operation, apparently within milliseconds. In this case, as the Wizard of Oz says, "They have one thing you haven't got."... and that would be a pretty cool language! According to experts in the Cardassian language,
"There is only one Cardassian font, but with two character styles in it because there were so few letters. Cardassian can be written in many different ways. Letters seems to be usable as: upside down, backwards, run together, and distorted into wide low 'fat' shapes. However, they are always the same set of letters." [53]
"Progressive evolution of more effective mind-parasites will have two aspects. New 'mutants' (either random or designed by humans) that are better at spreading will become more numerous. And there will be a ganging up of ideas that flourish in one another's presence, ideas that mutually support one another just as genes do and as I have speculated computer viruses may one day do. We expect that replicators will go around together from brain to brain in mutually compatible gangs. These gangs will come to constitute a package, which may be sufficiently stable to deserve a collective name such as Roman Catholicism or Voodoo. It doesn't too much matter whether we analogize the whole package to a single virus, to each one of the component parts to a single virus. The analogy is not that precise anyway, just as the distinction between a computer virus and a computer worm is nothing to get worked up about. What matters is that minds are friendly environments to parasitic, self-replicating ideas or information, and that minds are typically massively infected." [52]
The Need for a Universal Symbolic Language
Jump ahead 400 years to a time when humans are in intimate contact with alien races. The Star Trek universe is populated by starships of infinite variety with advanced technologies. A visit to Deep Space Nine, a space station outpost orbiting the planet Bajor near a stable wormwhole, places you bodily into the heart of Cardassian design. Control panels everywhere show a plethora of colorful symbols and animated displays. Amazingly, personnel working at displays in the Operations Center can monitor the smallest detail of the space station's operation, apparently within milliseconds. In this case, as the Wizard of Oz says, "They have one thing you haven't got."... and that would be a pretty cool language! According to experts in the Cardassian language,
"There is only one Cardassian font, but with two character styles in it because there were so few letters. Cardassian can be written in many different ways. Letters seems to be usable as: upside down, backwards, run together, and distorted into wide low 'fat' shapes. However, they are always the same set of letters." [53]
An example of the (fictional) Cardassian written language
Even in these primitive times, it would be useful for humanity to develop a symbolic language that can accomplish the following:
Such a language might be what Terrence W. Deacon conceives of in his book, "The Symbolic Species", in a section entitled "The Missing Simple Languages":
"The challenge to the complexity argument for human language origins rests on a simple thought experiment. Imagine a greatly simplified language, not a child's language that is a fragment of a more complicated adult language, but a language that is logically complete in itself, but with a very limited vocabulary and syntax, perhaps sufficient for only a very narrow range of activities. I do not mean 'language' in a metaphoric sense, the way that all communication systems are sometimes glossed as languages. But I also do not restrict my meaning to speech, or to a system whose organizational principles are limited to the sorts of grammatical rules found in modern languages. I mean language in the following very generic sense: a mode of communication based upon symbolic reference (the way words refer to things) and involving combinatorial rules that comprise a system for representing synthetic logical relationships among these symbols. Under this definition, manual signing, mathematics, computer 'languages,' musical compositions, religious ceremonies, systems of etiquette, and many rule-governed games might qualify as having the core attributes of language. More important, no more than a tiny 'vocabulary' of meaningful units and only two or three types of combinatorial rules would be necessary to fulfill these criteria." [54]
Knowledge Integration
At the root of all approaches to describing systems is the desire to tell a story, and the need to describe concepts in as succinct and meaningful a way as possible. A kind of "grand unifying theory" for describing systems is proposed to be needed. A proponent of this "integration of knowledge" is the Principia Cybernetica Project (PCP), an international organization. The Project says that it "aims to develop a complete philosophy or 'world-view', based on the principles of evolutionary cybernetics, and supported by collaborative computer technologies". The Principia Cybernetica (Web) organization states:
"Many of the concepts used by system theorists came from the closely related approach of cybernetics: information, control, feedback, communication...In fact cybernetics and systems theory study essentially the same problem, that of organization independent of the substrate in which it is embodied. Insofar as it is meaningful to make a distinction between the two approaches, we might say that systems theory has focused more on the structure of systems and their models, whereas cybernetics has focused more on how systems function, that is to say how they control their actions, how they communicate with other systems or with their own components, ... Since structure and function of a system cannot be understood in separation, it is clear that cybernetics and systems theory should be viewed as two facets of a single approach." [55]
It is clear from a review of the Principia Cybernetica's impressive and ambitious website that contributors to it have devoted a great deal of time and resources to the task. What strikes one is the heavy reliance on words to express their concepts. The concepts themselves could use graphic illustrations. Ironically, no previous method of using symbology to do so, is up to the task.
On a not-so-grand level, there are circumstances when the ability to "mix metaphors" might be handy. As is seen in many approaches to descrete event simulation, the symbology and methods developed to date do not easily allow the introduction of elements outside of an immediate set of grouped entities. In other words, a Tocher activity cycle dealing with the behavior of people waiting at a restaurant to be served by a waitress may not smoothly link with another activity cycle describing the interaction between parking attendents and the patrons at the same restaurant - especially if both stories need to be told simultaneously. Yet, this is precisely the kind of real world situations (or stories) that need to be dealt with.
Integrating knowledge systems can be difficult, although it is often another thing that must be done in the real world. Mental images of both objects and abstract data are synthesized by human beings, and both types of information must be processed at all times. An example of this synthesis is the way the pilot of an airplane needs to interact with its displays and controls. The Artificial Horizon Indicator presents a graphic image of the attitude of the airplane relative to the horizon. This most intuitive seeming instrument on the control panel (with its nice black-for-ground and blue-for-sky interface) actually provides only a small part of the overall situational picture. In fact, the Artificial Horizon Indicator, does not tell the pilot how fast the airplane is going, it does not indicate the rate of a turn, and probably most importantly, it does not tell the pilot how close the airplane is to the ground! Separate instruments for each of these pieces of information (speed, altitide, roll rate, and rate of climb) must be viewed, interpreted, and incorporated into a complete mental image by the pilot simultaneously. Unfortunately, each instrument presents the necessary information in different manners, even employing different units of measure. To add to the confusion, instruments rarely provide information instantaneously, so the pilot must interpolate their indications and regard the trends of their displays instead.
As regards to flying an airplane, there are many knowledge systems being integrated: navigation, radio communication, situational awareness, engine and fuel management, and flight controls. It would seem that in this age of desktop computers that can simulate flight so precisely, systems for intuitively displaying and controlling flight parameters could be developed. A symbolic language should allow for easy integration of knowledge systems, it should be able to "mix metaphors", and it should explain complex concepts by taking advantage of our intuitive abilities to understand structure without comprehending meaning.
The Time Factor
A simple definition of evolution is any process of change, or growth, over time. The study of the design and function of systems, whether human-based or machine-based, has traditionally had difficulty incorporating the element of time. The obvious reason is because attempts to describe attributes of a system almost always causes that system to be fixed in time. Yet, the evolution of systems can only truly be shown as unfolding over time.
Time has been described as the forgotten dimension.[56] For all practical (non-quantum, or relativistic) purposes, the arrow of time moves forward. Although we generally agree about the direction of time, we also regard time as having different qualities, such as slow, fast, quiet, short, long, endless, fleeting, spare, tight, and so on. When dealing with how time effects systems, we need to be very careful about defining the systems, then how time relates to them. For example, time can be quantified in seconds when describing a manufacturing process. How do you exactly describe the "time to move on" after a loved one dies, or "time for change" when charting events of historical significance?
The phrase "once upon a time" is not only used to preface a story, but as a signal to the listener to suspend our perception of time for a while. We become absorbed with the events, relationship between events, and the interactions between characters of the story rather than the exact minute something occurred. Human beings are good at switching between qualities of "real" and "percieved" time - machines are not. A symbolic language should be tolerant of our subjective use of time.
Degrees of Truth
The human mind works in metaphors. Aside from the ways we have of knowing about objects in the everyday world, we possess inferential tools such as the elements of logic, arithmetic, and probability. The spatial metaphor is found in language refer not only to changes, but also about unchanged states. We use space and motion as metaphors for other, more abstract ideas. Consider these examples:
The courier went from San Francisco to Ukiah.
The money finally went to my brother.
The light went from yellow to red.
The meeting went from 7:00 to 11:00.
In the first sentence it is clear that the courier actually moved from one place to another. The brother could have received the money by having it transferred to his bank account. Money did not actually have to change hands. The money certainly does not have to go anywhere. The traffic light is stationary, and meetings (even though we'd sometimes like them to go somewhere else) cannot travel at all.
People think in two modes: fuzzy stereotypes and rules (intuitive theories). Values, in human thought, can be represented as continuous, (and hence can represent the degree of truth) or the probability of truth of a statement, rather than being forced to describe conditions that are either absolutely true or absolutely false. It is therefore, essential to account for the quality of information passed between functional entities. Surface and deep structures are easily processed by our minds. We can quickly distinguish between "fuzzy" (representational) and "real" (objective) logic. A symbolic language should allow for both ways of thinking (and describing/learning).
The Evolutionary Imperative
It is clear that we are "wired" to perceive objects, shapes, colors, sound, and a host other stimuli in an evolutionarily-optimized manner. The preattentive and attentive processing that occurs in relation to color has analogues in our perception of symbols and objects. Deacon points out:
"No particular objects are intrinsically icons, indices, or symbols. They are interpreted to be so, depending on what is produces in response. In simple terms, the differences between iconic, indexical, and symbolic relationships derive from regarding things either in respect to their form, their correlations with other things, or their involvement in systems of conventional relationships."[57]
A universal symbolic language should be useful to anyone attempting to describe how something operates over time; to tell a story in a way that does not require a lot of words. It should allow a person interpreting the language product with an intuitive understanding of what is being described. They should be able to "peel away" layers of detail without losing sight of overall structure. Such a symbolic language might answer what Steven Pinker, in his book entitled "How the Mind Works", wonders about:
"Because a combinatorial system like a vocabulary can generate vast number of combinations, one might wonder whether human thoughts can be generated by a single system, a general purpose Esperanto of the mind."[58]
A universal symbolic language should take advantage of universal aspects of human perception.
Introduction to the LMSL
Inception
The Lewis-McKinley Symbolic Language (LMSL) was invented by Clovice A. Lewis, Jr. on March 31, 2000. It was inspired by a conversation with Roger McKinley, who was in need of a means to graphically depict abstract concepts he taught as part of his "Course in Fundamentals". The language allows its user to describe the evolution of practically any system using simple, intuitive symbology and/or color. The language allows its user to describe the evolution of practically any system using simple, intuitive symbology and/or color. The evolutionary aspect of the language was largely stimulated by the "meme" concept introduced in the groundbreaking book entitled "The Selfish Gene" by Richard Dawkins, which was first published in 1976.
Because development is time-dependent, to describe the evolution of any system requires that it is pictured for a brief moment within a series of successive moments... like the individual frames of a movie. As with a movie, the addition of color and sound enhance the story being conveyed. The LMSL is analogous to telling stories using a comic book format, where each panel represents a part of the story. It is left to the author to decide the amount of information, the arrangement of elements, and order of each panel to arrive at the most effective means of communication.
Elements
The basic elements of the LMSL are the following:
- Integrate knowledge systems
- Explain complex concepts intuitively
- Easily show evolutionary and time-related relationships between entities
- Express degrees of truth and accommodate "fuzzy logic"
- Take advantage of universal aspects of human perception
Such a language might be what Terrence W. Deacon conceives of in his book, "The Symbolic Species", in a section entitled "The Missing Simple Languages":
"The challenge to the complexity argument for human language origins rests on a simple thought experiment. Imagine a greatly simplified language, not a child's language that is a fragment of a more complicated adult language, but a language that is logically complete in itself, but with a very limited vocabulary and syntax, perhaps sufficient for only a very narrow range of activities. I do not mean 'language' in a metaphoric sense, the way that all communication systems are sometimes glossed as languages. But I also do not restrict my meaning to speech, or to a system whose organizational principles are limited to the sorts of grammatical rules found in modern languages. I mean language in the following very generic sense: a mode of communication based upon symbolic reference (the way words refer to things) and involving combinatorial rules that comprise a system for representing synthetic logical relationships among these symbols. Under this definition, manual signing, mathematics, computer 'languages,' musical compositions, religious ceremonies, systems of etiquette, and many rule-governed games might qualify as having the core attributes of language. More important, no more than a tiny 'vocabulary' of meaningful units and only two or three types of combinatorial rules would be necessary to fulfill these criteria." [54]
Knowledge Integration
At the root of all approaches to describing systems is the desire to tell a story, and the need to describe concepts in as succinct and meaningful a way as possible. A kind of "grand unifying theory" for describing systems is proposed to be needed. A proponent of this "integration of knowledge" is the Principia Cybernetica Project (PCP), an international organization. The Project says that it "aims to develop a complete philosophy or 'world-view', based on the principles of evolutionary cybernetics, and supported by collaborative computer technologies". The Principia Cybernetica (Web) organization states:
"Many of the concepts used by system theorists came from the closely related approach of cybernetics: information, control, feedback, communication...In fact cybernetics and systems theory study essentially the same problem, that of organization independent of the substrate in which it is embodied. Insofar as it is meaningful to make a distinction between the two approaches, we might say that systems theory has focused more on the structure of systems and their models, whereas cybernetics has focused more on how systems function, that is to say how they control their actions, how they communicate with other systems or with their own components, ... Since structure and function of a system cannot be understood in separation, it is clear that cybernetics and systems theory should be viewed as two facets of a single approach." [55]
It is clear from a review of the Principia Cybernetica's impressive and ambitious website that contributors to it have devoted a great deal of time and resources to the task. What strikes one is the heavy reliance on words to express their concepts. The concepts themselves could use graphic illustrations. Ironically, no previous method of using symbology to do so, is up to the task.
On a not-so-grand level, there are circumstances when the ability to "mix metaphors" might be handy. As is seen in many approaches to descrete event simulation, the symbology and methods developed to date do not easily allow the introduction of elements outside of an immediate set of grouped entities. In other words, a Tocher activity cycle dealing with the behavior of people waiting at a restaurant to be served by a waitress may not smoothly link with another activity cycle describing the interaction between parking attendents and the patrons at the same restaurant - especially if both stories need to be told simultaneously. Yet, this is precisely the kind of real world situations (or stories) that need to be dealt with.
Integrating knowledge systems can be difficult, although it is often another thing that must be done in the real world. Mental images of both objects and abstract data are synthesized by human beings, and both types of information must be processed at all times. An example of this synthesis is the way the pilot of an airplane needs to interact with its displays and controls. The Artificial Horizon Indicator presents a graphic image of the attitude of the airplane relative to the horizon. This most intuitive seeming instrument on the control panel (with its nice black-for-ground and blue-for-sky interface) actually provides only a small part of the overall situational picture. In fact, the Artificial Horizon Indicator, does not tell the pilot how fast the airplane is going, it does not indicate the rate of a turn, and probably most importantly, it does not tell the pilot how close the airplane is to the ground! Separate instruments for each of these pieces of information (speed, altitide, roll rate, and rate of climb) must be viewed, interpreted, and incorporated into a complete mental image by the pilot simultaneously. Unfortunately, each instrument presents the necessary information in different manners, even employing different units of measure. To add to the confusion, instruments rarely provide information instantaneously, so the pilot must interpolate their indications and regard the trends of their displays instead.
As regards to flying an airplane, there are many knowledge systems being integrated: navigation, radio communication, situational awareness, engine and fuel management, and flight controls. It would seem that in this age of desktop computers that can simulate flight so precisely, systems for intuitively displaying and controlling flight parameters could be developed. A symbolic language should allow for easy integration of knowledge systems, it should be able to "mix metaphors", and it should explain complex concepts by taking advantage of our intuitive abilities to understand structure without comprehending meaning.
The Time Factor
A simple definition of evolution is any process of change, or growth, over time. The study of the design and function of systems, whether human-based or machine-based, has traditionally had difficulty incorporating the element of time. The obvious reason is because attempts to describe attributes of a system almost always causes that system to be fixed in time. Yet, the evolution of systems can only truly be shown as unfolding over time.
Time has been described as the forgotten dimension.[56] For all practical (non-quantum, or relativistic) purposes, the arrow of time moves forward. Although we generally agree about the direction of time, we also regard time as having different qualities, such as slow, fast, quiet, short, long, endless, fleeting, spare, tight, and so on. When dealing with how time effects systems, we need to be very careful about defining the systems, then how time relates to them. For example, time can be quantified in seconds when describing a manufacturing process. How do you exactly describe the "time to move on" after a loved one dies, or "time for change" when charting events of historical significance?
The phrase "once upon a time" is not only used to preface a story, but as a signal to the listener to suspend our perception of time for a while. We become absorbed with the events, relationship between events, and the interactions between characters of the story rather than the exact minute something occurred. Human beings are good at switching between qualities of "real" and "percieved" time - machines are not. A symbolic language should be tolerant of our subjective use of time.
Degrees of Truth
The human mind works in metaphors. Aside from the ways we have of knowing about objects in the everyday world, we possess inferential tools such as the elements of logic, arithmetic, and probability. The spatial metaphor is found in language refer not only to changes, but also about unchanged states. We use space and motion as metaphors for other, more abstract ideas. Consider these examples:
The courier went from San Francisco to Ukiah.
The money finally went to my brother.
The light went from yellow to red.
The meeting went from 7:00 to 11:00.
In the first sentence it is clear that the courier actually moved from one place to another. The brother could have received the money by having it transferred to his bank account. Money did not actually have to change hands. The money certainly does not have to go anywhere. The traffic light is stationary, and meetings (even though we'd sometimes like them to go somewhere else) cannot travel at all.
People think in two modes: fuzzy stereotypes and rules (intuitive theories). Values, in human thought, can be represented as continuous, (and hence can represent the degree of truth) or the probability of truth of a statement, rather than being forced to describe conditions that are either absolutely true or absolutely false. It is therefore, essential to account for the quality of information passed between functional entities. Surface and deep structures are easily processed by our minds. We can quickly distinguish between "fuzzy" (representational) and "real" (objective) logic. A symbolic language should allow for both ways of thinking (and describing/learning).
The Evolutionary Imperative
It is clear that we are "wired" to perceive objects, shapes, colors, sound, and a host other stimuli in an evolutionarily-optimized manner. The preattentive and attentive processing that occurs in relation to color has analogues in our perception of symbols and objects. Deacon points out:
"No particular objects are intrinsically icons, indices, or symbols. They are interpreted to be so, depending on what is produces in response. In simple terms, the differences between iconic, indexical, and symbolic relationships derive from regarding things either in respect to their form, their correlations with other things, or their involvement in systems of conventional relationships."[57]
A universal symbolic language should be useful to anyone attempting to describe how something operates over time; to tell a story in a way that does not require a lot of words. It should allow a person interpreting the language product with an intuitive understanding of what is being described. They should be able to "peel away" layers of detail without losing sight of overall structure. Such a symbolic language might answer what Steven Pinker, in his book entitled "How the Mind Works", wonders about:
"Because a combinatorial system like a vocabulary can generate vast number of combinations, one might wonder whether human thoughts can be generated by a single system, a general purpose Esperanto of the mind."[58]
A universal symbolic language should take advantage of universal aspects of human perception.
Introduction to the LMSL
Inception
The Lewis-McKinley Symbolic Language (LMSL) was invented by Clovice A. Lewis, Jr. on March 31, 2000. It was inspired by a conversation with Roger McKinley, who was in need of a means to graphically depict abstract concepts he taught as part of his "Course in Fundamentals". The language allows its user to describe the evolution of practically any system using simple, intuitive symbology and/or color. The language allows its user to describe the evolution of practically any system using simple, intuitive symbology and/or color. The evolutionary aspect of the language was largely stimulated by the "meme" concept introduced in the groundbreaking book entitled "The Selfish Gene" by Richard Dawkins, which was first published in 1976.
Because development is time-dependent, to describe the evolution of any system requires that it is pictured for a brief moment within a series of successive moments... like the individual frames of a movie. As with a movie, the addition of color and sound enhance the story being conveyed. The LMSL is analogous to telling stories using a comic book format, where each panel represents a part of the story. It is left to the author to decide the amount of information, the arrangement of elements, and order of each panel to arrive at the most effective means of communication.
Elements
The basic elements of the LMSL are the following:
|
Entity - a constituent element of a system
|
|
|
Interaction - the type of communication or contact between entities
|
|
Mode - the effect of an entity on a system at a given point in time
Condition - the "status" of an entity
Timeframe - an arbitrary unit of time within which interaction occurs
between entities
System - set of entities or parts forming a whole
Condition - the "status" of an entity
Timeframe - an arbitrary unit of time within which interaction occurs
between entities
System - set of entities or parts forming a whole
A simple way of visualizing how the LMSL works is to imagine everything as a story unfolding over time (an evolutionary process). Entities are people, places, and things which populate the story (the system). The way communication and action between entities is accomplished, and how the entities respond to that communication or action is interaction. Whether an entity has a beneficial, harmful, or neutral effect in the system is its mode; the "health" of the entity (whether it is feeling good, half-fueled, or just about to die) is its condition. A timeframe is any segment of time that allows for a meaningful understanding of changes in a system. These time segments are called "Schemas" when a two-dimensional representation of a system is used, and "States" when an animated, or 3-Dimensional representation of the system is used.
The LMSL is a subjective language; definitions and meanings are entirely left to the author. The only requirements of the language are that any symbology employed is self-consistent, a legend is always included, and that the syntax and rules of the language are observed.
The LMSL is designed to allow a person to create graphic representations of abstract concepts using a variety of tools, from pencil and paper to sophisticated computer-generated programs. A few standard symbol sets are described in this document. The power and flexibility of the language lies in the fact that a user can create their own formats and variations of styles. Future implementations of the LMSL will include computer programs that will automatically create Schema and State depictions based upon user input of definitions, symbology, and timeframes. Depictions will range from simple black and white line drawings to fully interactive 3-D models and animation with sound and color.
Legend
The legend is central to an LMSL chart. The legend below shows the standard symbols used with the LMSL, and their meanings.
The LMSL is a subjective language; definitions and meanings are entirely left to the author. The only requirements of the language are that any symbology employed is self-consistent, a legend is always included, and that the syntax and rules of the language are observed.
The LMSL is designed to allow a person to create graphic representations of abstract concepts using a variety of tools, from pencil and paper to sophisticated computer-generated programs. A few standard symbol sets are described in this document. The power and flexibility of the language lies in the fact that a user can create their own formats and variations of styles. Future implementations of the LMSL will include computer programs that will automatically create Schema and State depictions based upon user input of definitions, symbology, and timeframes. Depictions will range from simple black and white line drawings to fully interactive 3-D models and animation with sound and color.
Legend
The legend is central to an LMSL chart. The legend below shows the standard symbols used with the LMSL, and their meanings.
Rules
Schemas
The interaction between entities is illustrated within an arbitrary timeframe that best explains the significant events and/or interactions which occur. 2-Dimensional representations of a timeframe are called Schemas. Thus, Schemas can be thought of as the frames of a comic strip, where each frame tells a part of the story.
Labeled Entities with Mode Shapes and No Conditions
In this example numbers (1-6) are used to label the identity of an entity and, according to LMSL rules, shapes are used to denote the entity mode (positive, negative, neutral, or terminated. A variation could be to color the numbered labels (or the shapes) to show the condition of entities ("green" - fully functional, "yellow" - partially functional, or "red" - terminal).
- Time is always assumed to move forward (e.g. events progress in time).
- The interaction between entities is illustrated within an arbitrary timeframe that best explains the significant events and/or interactions which occur. 2-Dimensional representations divide timeframes into Schemas. 3-Dimensional representations divide timeframes into States.
- Interactions between entities can occur synchronously and/or asynchronously.
- A Neutral entity cannot effect a transformation by itself, but can serve as a catalyst for the creation of a positive or negative entity.
- Transformation cannot occur if it can affect the entity that produced the transformation within the same Schema or State.
- Duplication (or replication) can only occur as a result of positive transformation and/or error-free transmission.
- An originating entity cannot be transformed by a copy of itself within the same schema or state.
- An entity may, or may not, make an "internal" transition from one mode (positive, negative, or neutral) to another. Transformations are always an external power which actively seeks to force an entity to change its mode.
- If colors are used to identify entities then shapes identify their modes (positive, negative, or neutral). If shapes (and/or lables) are used to identify entities, then symbols ("+" for positive, "-" for negative, and "/" for neutral) identify their modes; and colors can be used to identify their condition (fully functional, partially functional, or terminal). Any self-consistent variation of symbols, interactions, and colors is allowable.
- A Legend should always accompany an LMSL illustration.
Schemas
The interaction between entities is illustrated within an arbitrary timeframe that best explains the significant events and/or interactions which occur. 2-Dimensional representations of a timeframe are called Schemas. Thus, Schemas can be thought of as the frames of a comic strip, where each frame tells a part of the story.
Labeled Entities with Mode Shapes and No Conditions
In this example numbers (1-6) are used to label the identity of an entity and, according to LMSL rules, shapes are used to denote the entity mode (positive, negative, neutral, or terminated. A variation could be to color the numbered labels (or the shapes) to show the condition of entities ("green" - fully functional, "yellow" - partially functional, or "red" - terminal).
Shaped Entities with Mode Symbols and No Conditions
In this Schema example shapes are used to denote the identity of an entity and symbols are used to denote the entity mode (positive, negative, neutral, or terminated). LMSL rules allow colors to be used to denote the condition of an entity. Note that this example also used grey lines (instead of "dashed" lines) to denote the "information" interaction between entities. Also note that each version of the Schemas show exactly the same information. The ability to mix symbology is one of the keys to the power and flexibility of the language.
In this Schema example shapes are used to denote the identity of an entity and symbols are used to denote the entity mode (positive, negative, neutral, or terminated). LMSL rules allow colors to be used to denote the condition of an entity. Note that this example also used grey lines (instead of "dashed" lines) to denote the "information" interaction between entities. Also note that each version of the Schemas show exactly the same information. The ability to mix symbology is one of the keys to the power and flexibility of the language.
States
The interaction between entities is illustrated within an arbitrary timeframe that best explains the significant events and/or interactions which occur. 3-Dimensional representations of a timeframe are called States. Using 3-D objects like the one depicted below, a user can manipulate the object and see all the interactions that might be hidden, or difficult to illustrate in a 2-Dimensional drawing. In this example color is used to denote the identity of an entity and shapes are used to denote the entity mode (positive, negative, neutral, or terminated). Other information can be displayed by touching an entity, such as its condition (fully functional, partially functional, or terminal), as well as its name.
The interaction between entities is illustrated within an arbitrary timeframe that best explains the significant events and/or interactions which occur. 3-Dimensional representations of a timeframe are called States. Using 3-D objects like the one depicted below, a user can manipulate the object and see all the interactions that might be hidden, or difficult to illustrate in a 2-Dimensional drawing. In this example color is used to denote the identity of an entity and shapes are used to denote the entity mode (positive, negative, neutral, or terminated). Other information can be displayed by touching an entity, such as its condition (fully functional, partially functional, or terminal), as well as its name.
How the LMSL Can Be Used
A separate book has been written which provides a detailed explanation of the LMSL, along with examples of its use. The LMSL can be used for the following:
A separate book has been written which provides a detailed explanation of the LMSL, along with examples of its use. The LMSL can be used for the following:
- Model events
- Tell stories
- Describe complex relationships
- Explain and illustrate complex abstractions
- Visualize the internal logic (or lack thereof) of communications
- Troubleshoot problems
- Simulate discrete events